(So far, 323 people got it right out of 622 for a success rate of 51%)
(Thank you to Clive "Max" Maxfield for submitting this question. Make sure to have a look at his "Cool Beans" blog and to read everything by Max imagining a strong British accent.)
This is a digital logic problem. Let's assume we have a "black box" with three inputs called A, B, and C, and three outputs called not_A, not_B, and not_C. We want each of the outputs to be the logical negation of its corresponding input (e.g., not_A = !A).
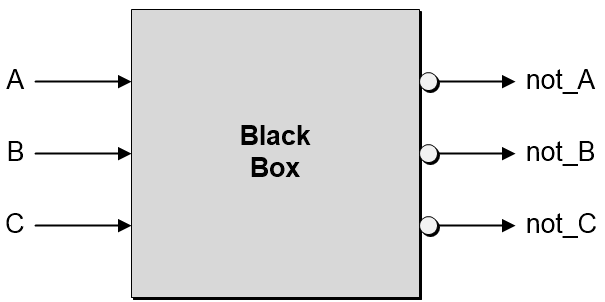
The question is, is this possible using only AND and OR gates along with just two (2) NOT gates, but no NAND, NOR, XOR, or XNOR gates?
- Comments
- Write a Comment Select to add a comment

The output equations generalize easily, for example for 5 inputs:
not_A = 0ones + (1one & (B + C + D + E)) + (2ones & (BC + BD + BE + CD + CE + DE)) + (3ones & (BCD + BCE + BDE + CDE)) + (4ones & (BCDE));
// swap A and B to get the next equation:
not_B = 0ones + (1one & (A + C + D + E)) + (2ones & (AC + AD + AE + CD + CE + DE)) + (3ones & (ACD + ACE + ADE + CDE)) + (4ones & (ACDE));
// swap B and C to get the next equation (and so on)
not_C = 0ones + (1one & (A + B + D + E)) + (2ones & (AB + AD + AE + BD + BE + DE)) + (3ones & (ABD + ABE + ADE + BDE)) + (4ones & (ABDE));
not_D = 0ones + (1one & (A + B + C + E)) + (2ones & (AB + AC + AE + BC + BE + CE)) + (3ones & (ABC + ABE + ACE + BCE)) + (4ones & (ABCE));
not_E = 0ones + (1one & (A + B + C + D)) + (2ones & (AB + AC + AD + BC + BD + CD)) + (3ones & (ABC + ABD + ACD + BCD)) + (4ones & (ABCD));
And then the rest is just a matter of writing 1one, 2ones, 3ones, 4ones, etc., which are symmetric boolean functions of the inputs and showing you can write these with some number k of NOT gates.
Start with the symmetric functions that are the sum of products Sj, taking products of all combinations of j of them at a time; for example for 5 inputs:
S1 = A + B + C + D + E = at least 1 one
S2 = AB + AC + AD + AE + BC + BD + BE + CD + CE + DE = at least 2 ones
S3 = ABC + ABD + ABE + ACD + ACE + ADE + BCD + BCE + BDE + CDE = at least 3 ones
S4 = ABCD + ABCE + ABDE + ACDE + BCDE = at least 4 ones
S5 = ABCDE = at least 5 ones
now decompose into binary bits of the number of ones, for example:
B2 = S4 = (either 4 or 5 ones = the highest bit of the number of ones)
and we also calculate !B2 = at most 3 ones, so there's our first not gate.
B1 = S2 & !S4 = S2 & !B2 = (either 2 or 3 ones = the middle bit of the number of ones)
and we also calculate !B1 so there's our second not gate.
B0 = odd number of gates = A ^ B ^ C ^ D ^ E = (either 1 or 3 or 5 ones = last bit of the number of ones)
Each odd number of gates we can calculate from the values we have already:
1 one = S1 & !B1 & !B2
3 ones = S3 & !B2
5 ones = S5
so B0 = (S1 & !B1 & !B2) | (S3 & !B2) | S5
and we also calculate !B0, so there's our third not gate.
Now we can calculate the even number of gate counts:
0ones = !B0 & !B1 & !B2
2ones = !B0 & B1 & !B2
4ones = !B0 & !B1 & B2
The gate counts work similarly for 7 inputs, which still require only 3 NOT gates:
B2 = S4 = (at least 4 ones), and we calculate !B2
B1 = (S2 & !S4) + S6 = (two or three or six or seven ones = middle bit of the number of ones), and we calculate !B1
1 one = S1 & !B2 & !B1
3 ones = S3 & !B2
5 ones = S5 & !B1
7 ones = S7
B0 = (1 one) + (3 ones) + (5 ones) + (7 ones), and we can calculate !B0
and the even number of gate counts fall out just as before:
0ones = !B0 & !B1 & !B2
2ones = !B0 & B1 & !B2
4ones = !B0 & !B1 & B2
6ones = !B0 & B1 & B2
So it looks like you need a number of NOT gates equal to bit_width(n) = 1 + floor(log2(n))
Of course, Gauss probably proved this in 1806 in a notebook he stuffed in a drawer for the rest of his life.

Excellent work!
According to your building rule we need 4 NOTs for >=8 inputs, 5 NOTs for >=16 inputs, 6 NOTs for >=32 inputs, and so on.

Wow!!! This is a fantastic piece of work -- now my head really hurts!!!
Can you show a diagram of the gates please. I don’t understand what you’ve writte

I'm sorry -- this would be really messy if we drew it out in logic gates -- but you could easily draw out the individual stages if that makes it easier for you to visualize things.

Should be this -- yes, somewhat messy. Don't think if we have four inputs ...


... and here the truth table. Yes, it works, but it is really a veeeeeeeeeery academic solution!


Awesome -- thanks for doing this (this is one of my favorite logic problems)
The gate picture for the proposed solution is quite messy, as it involves several layers of gates. You can do it yourself of course from the equations---I tried and it was a complete spaghetti, and the equations actually explain the idea behind the solution a little better.
Having said that, I came up with a different, simpler design:
Aout = not Ain
Bout = not(Bin and Cin) and Bin
Cout = not(Bin and Cin) and Cin
which is fairly easy to draw, as it involves only five total gates.
It works because not(Bin and Cin) is notBin or notCin by de Morgan laws, and when you OR it with e.g. Bin you can cancel out Bin OR notBin, so notCin is what's left.

This sounds great (happy face) -- but I don't think it works (sad face). Consider the following truth table (I'm using Bi and Bo etc. for in and out to keep things short, also ! & | for NOT, AND, OR):
Bi Ci | (Bi & Ci) | !(Bi & Ci) | Bo = !(Bi & Ci) & Bi | !Bi
------+-----------+------------+----------------------+-----
0 0 | 0 | 1 | 0 | 1
0 1 | 0 | 1 | 0 | 1
1 0 | 0 | 1 | 1 | 0
1 1 | 1 | 0 | 0 | 0
^ ^
| |
What we get --------------' |
|
What we want --------------------------'

Hi Max,
if I did the right thing, you should receive a notification email to let you know about this comment.
Please let me know if you received it, thanks!
Stephane

To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:























