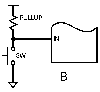
Integer PI control with integrator anti-windup
/**
* @file
* Proportional-integral (PI) control law.
*
* This module implements a simple position-type PI controller:
* <pre>
* u = [ kp * e + ki * sum(e) ] >> shift
* </pre>
* <tt>shift</tt> is a right bit shift used to scale the output of the
* controller down from the 32-bit intermediate result.
*
* An anti-windup provision is implemented on the PI integrator to prevent
* deep saturation (aka integrator windup):
* - The new control output with the latest integrator value is computed.
* - If the control output exceeds either output limit, <i>and</i> the latest
* change in the integrator is in the same direction, then the new integrator
* value is not saved for the next call.
* - Otherwise, the integrator is saved for the next call.
*/
#include <stdbool.h>
#include "pi_control.h"
/**
* Proportional-integral (PI) control law.
*
* @param[in,out] p control parameter and state structure
* @param[in] e error signal
*
* @return control output <code>u</code>
*/
int pi_control (struct PIControl *p, int e)
{
bool int_ok; /* Whether or not the integrator should update */
long new_i; /* Proposed new integrator value */
long u; /* Control output */
/* Compute new integrator and the final control output. */
new_i = p->i + e;
u = (p->kp * (long)e + p->ki * new_i) >> p->shift;
/* Check for saturation. In the event of saturation in any one direction,
inhibit saving the integrator if doing so would deepen the saturation. */
int_ok = true;
/* Positive saturation? */
if (u > p->max)
{
/* Clamp the output */
u = p->max;
/* Error is the same sign? Inhibit integration. */
if (e > 0)
{
int_ok = false;
}
}
/* Repeat for negative sign */
else if (u < p->min)
{
u = p->min;
if (e < 0)
{
int_ok = false;
}
}
/* Update the integrator if allowed. */
if (int_ok)
{
p->i = new_i;
}
return (int)u;
}
/**
* Initializes the PI control.
*
* This function resets the PI integrator to zero.
*
* @param[in,out] p control parameter structure
*/
void pi_control_init (struct PIControl *p)
{
p->i = 0L;
}
/* Header file */
#if !defined(_PI_CONTROL_H)
#define _PI_CONTROL_H
/**
* @file
* Proportional-integral (PI) control law header file.
*/
/** PI control data structure. This structure contains configuration (the
proportional and integral gain, plus a final divisor), output limits, and
an integration accumulator (the PI controller's state variable). */
struct PIControl
{
int kp; /**< Proportional gain constant */
int ki; /**< Integral gain constant */
unsigned char shift; /**< Right shift to divide */
int max; /**< Maximum value */
int min; /**< Minimum value */
long i; /**< Current integrator value */
};
/* Prototypes */
int pi_control (struct PIControl *p, int e);
void pi_control_init (struct PIControl *p);
#endif /* _PI_CONTROL_H */I2C driver
/*
File: I2C_drive.h
*/
#ifndef __I2C_H
#define __I2C_H
#include <AT89X51.H>
#include <INTRINS.H>
typedef unsigned char ubyte;
/*
****************************************************
* I2C Bus Configuration
*
****************************************************
*/
#define sda P1_0
#define scl P1_1
#define HOLD _nop_(); _nop_(); _nop_()
void send_stop();
void master(ubyte);
void send_byte(ubyte);
void send_data(ubyte, ubyte, ubyte, ubyte *);
ubyte recv_byte(ubyte);
void recv_data(ubyte, ubyte, ubyte, ubyte *);
#endif
----------------------------------------------------------
/*
File: I2C_drive.c
*/
#include "I2C_drive.h"
bit i2c_busy, no_ack, bus_fault;
ubyte bdata a;
sbit LSB=a ^ 0;
sbit MSB=a ^ 7;
/*
************************************
* Sending Stop Condition
************************************
*/
void send_stop()
{
sda = 0;
scl = 1;
HOLD;
sda = 1;
i2c_busy = 0;
}
/*
************************************
* I2C Start Condition
*
* NOTE: need to use it.
************************************
*/
void master(ubyte slave_addr)
{
i2c_busy = 1;
no_ack = 0;
bus_fault = 0;
if(!scl||!sda)
bus_fault = 1;
else
{
sda = 0;
HOLD;
scl = 0;
HOLD;
send_byte(slave_addr);
}
}
/*
************************************
* Sending a byte on I2C Bus
************************************
*/
void send_byte(ubyte i2c_data)
{
ubyte i;
a=i2c_data;
for(i=0;i<8;i++)
{
scl=0;
HOLD;
sda=MSB;
a<<=1;
_nop_();
scl=1;
HOLD;
scl=0;
}
sda = 1;
scl = 1;
HOLD;
if(!sda)
{
scl = 0;
HOLD;
}
else
{
no_ack = 1;
scl = 0;
HOLD;
}
}
/*
****************************************************
* Sending data on I2C bus
*
* Usage:
* send_data(0xD0,0x10, 0x20, send_buffer)
*
* 0XD0: Slave address, Must me with write bit
* 0x10: Starting address, or sub-address
* 0x20: number of bytes to send
* send_buffer: adress of the buffer pointer
*
*****************************************************
*/
void send_data(ubyte slave_add, ubyte sub_add, ubyte bytes, ubyte *data_in)
{
master(slave_add);
send_byte(sub_add);
if(no_ack)
send_stop();
else
{
for(bytes;bytes>0;bytes--)
{
send_byte(*data_in++);
if(no_ack)
break;
}
send_stop();
}
}
/*
*********************************************
* Recieve a single byte from I2C Bus
*
* Note: if you are going to recieve
* a single byte then the passing
* argument should be 1.
*
*********************************************
*/
ubyte recv_byte(ubyte cnt)
{
ubyte i,rcv_data;
for(i=0;i<8;i++)
{
sda=1;
scl=1;
HOLD;
LSB=sda;
if(i<7)
a<<=1;
HOLD;
scl=0;
HOLD;
}
if(cnt==1)
sda = 1;
else
sda = 0;
scl =1;
HOLD;
scl = 0;
sda = 1;
HOLD;
rcv_data = a;
return rcv_data;
}
/*
****************************************************
* Recieving bulk data on I2C bus
*
* Usage:
* recv_data(0xD0,0x10, 0x20, send_buffer)
*
* 0XD0: Slave address, Must me with write bit
* 0x10: Starting address, or sub-address
* 0x20: number of bytes to recieve
* send_buffer: adress of the recieve buffer
* pointer
*
*****************************************************
*/
void recv_data(ubyte slave_add, ubyte sub_add, ubyte byte_cnt, ubyte *recv_buf)
{
ubyte i;
scl = sda = 1;
master(slave_add);
send_byte(sub_add);
slave_add+=1;
scl = sda = 1;
master(slave_add);
if(no_ack)
{
send_stop();
goto exit;
}
for(i=0;i<byte_cnt;i++)
recv_buf[i]=recv_byte(byte_cnt-i);
send_stop();
exit:;
}I2C driver using bit bang
typedef struct
{
unsigned int PIN0:1;
unsigned int PIN1:1;
unsigned int PIN2:1;
unsigned int PIN3:1;
unsigned int PIN4:1;
unsigned int PIN5:1;
unsigned int PIN6:1;
unsigned int PIN7:1;
} PORT;
/* TODO: Example address shown, but the proper address */
#define PORT0 *(volatile PORT *)0x1234
/* Define the port used for I2C data and clk as shown above to access them pin wise */
#define I2C_DATA PORT0.PIN0
#define I2C_CLK PORT0.PIN1
#define HIGH 1
#define LOW 0
/* I2C Start - bit bang */
void I2C_START(void)
{
/* I2C Start condition, data line goes low when clock is high */
I2C_DATA = HIGH;
I2C_CLK = HIGH;
I2C_DATA = LOW;
I2C_CLK = LOW;
}
/* I2C Stop - bit bang */
void I2C_STOP (void)
{
/* I2C Stop condition, clock goes high when data is low */
I2C_CLK = LOW;
I2C_DATA = LOW;
I2C_CLK = HIGH;
I2C_DATA = HIGH;
}
/* I2C Write - bit bang */
void I2C_WRITE(unsigned char data)
{
unsigned char outBits;
unsigned char inBit;
/* 8 bits */
for(outBits = 0; outBits < 8; outBits++)
{
if(data & 0x80)
I2C_DATA = 1;
else
I2C_DATA = 0;
data <<= 1;
/* Generate clock for 8 data bits */
SCLK = HIGH;
SCLK = LOW;
}
/* Generate clock for ACK */
I2C_CLK = HIGH;
/* Wait for clock to go high, clock stretching */
while(I2C_CLK);
/* Clock high, valid ACK */
inBit = I2C_DATA;
I2C_CLK = LOW;
}
unsigned char I2C_READ (void)
{
unsigned char inData, inBits;
inData = 0x00;
/* 8 bits */
for(inBits = 0; inBits < 8; inBits++)
{
inData <<= 1;
I2C_CLK = HIGH;
inData |= I2C_DATA;
I2C_CLK = LOW;
}
return inData;
}
/* Examble for writing to I2C Slave */
void writeI2CSlave (unsigned char data)
{
/* Start */
I2C_START();
/* Slave address */
I2C_WRITE(0xAA)
/* Slave control byte */
I2C_WRITE(0xBB);
/* Slave data */
I2C_WRITE(data);
/* Stop */
I2C_STOP();
}
/* Examble for reading from I2C Slave */
unsigned char readI2CSlave(unsigned char data)
{
unsigned char inData;
/* Start */
I2C_START();
/* Slave address */
I2C_WRITE(0xAA);
/* Slave control byte */
I2C_WRITE(data);
/* Stop */
I2C_STOP();
/* Start */
I2C_START();
/* Slave address + read */
I2C_WRITE(0xAA | 1);
/* Read */
inData = I2C_READ();
return inData;
}PID Control
// PID Control program by Bill Keenan, Melbourne
// Throttle PID loop stuff
#define Umin -1022
#define Umax 1022
#define Kp 0.5 //
#define Ki 0.005 //
#define Kd 1.25 //
float U0 = 0;
float integ; // integration part of PID-loop must be saved
float ep; // previous error used for differential error (e - ep)
/*****************************************************************************/
float prop, junk, der; //
// junk, U0, Umax, Umin, Kp, Ki, err.
int throttle_pidloop(int realpos) // PID-loop calc
// integ - integral part of controller
// ep - preceding control error
// realpos - throttle position feedback
// Besides this function uses global variables such as:
// Kp,Ki,Kd,U0 - constants of controller;
// accel_use - setpoint
// Umin,Umax - range of the output control signal
{
int output;
float error; // actual control error
error = (float)(accel_use - realpos); // calculation of actual error
der = ((error - ep) * Kd);
prop = error * Kp; // calculation of proportional part
if(prop > 1022)
{
prop = 1022;
}
if(prop < -1022)
{
prop = -1022;
}
junk = error * Ki; // calculation of integral part
integ = integ + junk;
if ((int)integ > Umax)
{
integ = (float)Umax;
}
else if ((int)integ < Umin)
{
integ = (float)Umin;
}
output = (int)(prop + integ + der);
if (output > Umax)
{
output = Umax;
}
else if (output < Umin)
{
output = Umin;
}
ep = error; // new error
return(output); // return the object controlling magnitude
}Interface matrix Keypad
/Keypad connection:
#define col0 PIN_B3
#define col1 PIN_B2
#define col2 PIN_B1
#define col3 PIN_B0
#define row0 PIN_B7
#define row1 PIN_B6
#define row2 PIN_B5
#define row3 PIN_B4
#define num_col 4
// Keypad layout:
char const KEYS[4][4] = {{1,2,3,13},
{4,5,6,14},
{7,8,9,15},
{11,10,12,16}};
void init_keypad()
{
output_high(row0);
output_high(row1);
output_high(row2);
output_high(row3);
output_low(col0);
output_low(col1);
output_low(col2);
output_low(col3);
}
short int ALL_ROWS (void)
{
if (input (row0) & input (row1) & input (row2) & input (row3))
return (0);
else
return (1);
}
//Will return a key value if pressed or 0 if not
int8 get_key()
{
int8 row,col=0;
do
{
switch (col)
{
case 0 :
output_low(col0);
output_high(col1);
output_high(col2);
output_high(col3);
break;
case 1 :
output_high(col0);
output_low(col1);
output_high(col2);
output_high(col3);
break;
case 2 :
output_high(col0);
output_high(col1);
output_low(col2);
output_high(col3);
break;
case 3 :
output_high(col0);
output_high(col1);
output_high(col2);
output_low(col3);
break;
}
if(!input (row0))
row=1;
else if(!input (row1))
row=2;
else if(!input (row2))
row=3;
else if(!input (row3))
row=4;
else
row=0;
col++;
}while(!row && col<num_col);
if(row)
return KEYS[row-1][col-1];
else
return 0;
}
//function waits until any key is pressed and released.
int8 get_key_released()
{
int8 _key_temp ;
do
{
_key_temp=get_key();
}while(!_key_temp);
init_keypad();
do
{
while(ALL_ROWS());
delay_ms(50);
}
while(ALL_ROWS());
return _key_temp;
}1D and 2D table lookup
/**
* @file
* Table lookup with interpolation (1-D and 2-D).
*
* This is a 1/2-D table lookup facility. Each routine looks up data in a table
* structure, interpolating as needed between data points. The 2-D version
* looks up along 2 axes and interpolates in two dimensions.
*
* <h2>Limitations</h2>
* - The table axes (input values) must monotonically increase, or the lookup
* will fail.
* - The index data type is nominally 8 bits, limiting the table length to
* 256 elements. Change <code>index_t</code> if larger tables are needed.
*/
#include <stdint.h>
#include <stdbool.h>
#include "lookup.h"
/** Index data type */
typedef uint8_t index_t;
/**
* 1-D table lookup.
*
* This function performs a 1-D table lookup with interpolation. The output
* value is clamped to either of the table end values when the input value is
* out of bounds.
*
* @param[in] t table data structure
* @param[in] ix input (X-axis) value
* @param[out] o output data
*
* @retval true if the lookup result is suspect due to clipping
* @retval false on successful lookup
*/
bool lookup1d (Table1d *t, int ix, int *o)
{
index_t i;
/* ------------------------------------------------------------------------ */
/* Off the end of the table */
if (ix > t->columns[t->ncols - 1])
{
*o = t->table[t->ncols - 1];
return true;
}
/* Off beginning of the table */
else if (ix < t->columns[0])
{
*o = t->table[0];
return true;
}
/* Within the bounds of the table */
for (i = 0; i < t->ncols - 1; ++i)
{
if ( ix >= t->columns[i]
&& ix <= t->columns[i + 1])
{
/* Output (table) low value */
int o_low = t->table[i];
/* Input (X-axis) low value */
int i_low = t->columns[i];
/* Spead between the two adjacent input values */
int i_delta = t->columns[i + 1] - t->columns[i];
/* Spread between the two adjacent table output values */
int o_delta = t->table[i + 1] - t->table[i];
/* Prevent division by zero. We could get here if two consecutive
input values in the table are the same. */
if (o_delta == 0)
{
*o = o_low;
return true;
}
*o = o_low + ((ix - i_low) * (long)o_delta) / i_delta;
return false;
}
}
/* Didn't find it (we shouldn't ever get here). */
return true;
}
/**
* 2-D table lookup.
*
* This function performs a 2-D table lookup with interpolation. The output
* value is clamped to either of the table end values when the input value is
* out of bounds.
*
* @param[in] t table data structure
* @param[in] ix input (X-axis) value
* @param[in] iy input (Y-axis) value
* @param[out] o output value
*
* @retval true if the lookup result is suspect due to clipping
* @retval false on successful lookup
*/
bool lookup2d (Table2d *t, int ix, int iy, int *o)
{
/* The lower X and Y coordinates of the interpolation box */
index_t i, j;
/* Set whenever one of the lookups goes off the end of the table */
bool is_fault = false;
/* ------------------------------------------------------------------------ */
/* X axis coordinate lookup */
/* Off the end of the table */
if (ix > t->columns[t->ncols - 1])
{
/* Pretend the input value is right at the table edge so that interpolation
works as expected */
ix = t->columns[t->ncols - 1];
i = t->ncols - 1;
is_fault = true;
}
/* Off beginning of the table */
else if (ix < t->columns[0])
{
ix = t->columns[0];
i = 0;
is_fault = true;
}
/* Within the bounds of the table */
else
{
for (i = 0; i < t->ncols - 1; ++i)
{
if ( ix >= t->columns[i]
&& ix <= t->columns[i + 1])
{
break;
}
}
}
/* ------------------------------------------------------------------------ */
/* Y axis coordinate lookup */
/* Off the bottom of the table */
if (iy > t->rows[t->nrows - 1])
{
iy = t->rows[t->nrows - 1];
j = t->nrows - 1;
is_fault = true;
}
/* Off the top of the table */
else if (iy < t->rows[0])
{
iy = t->rows[0];
j = 0;
is_fault = true;
}
/* Within the bounds of the table */
else
{
for (j = 0; j < t->nrows - 1; ++j)
{
if ( iy >= t->rows[j]
&& iy <= t->rows[j + 1])
{
break;
}
}
}
/* ------------------------------------------------------------------------ */
/* 2-D interpolation */
/* At this point we know that the input X value is between
column[i] and column[i+1] and that the input Y value is between
row[j] and row[j+1]. Therefore we have a rectangle in which we need
to interpolate.
To do the interpolation, we first interpolate between column i and
column i+1 on the upper row j. Then, we interpolate between the same
columns on row j+1. Finally, we interpolate vertically between the two
rows based on the input Y value.
row0 is the upper row data and row1 is the lower (higher subscript) row
data. */
{
const int *row0 = &t->table[j * t->ncols];
const int *row1 = &row0[t->ncols];
/* Difference between the two adjacent column values */
int i_delta = t->columns[i + 1] - t->columns[i];
/* Difference between the two adjacent row values */
int j_delta = t->rows[j + 1] - t->rows[j];
/* Low column value */
int i_low = t->columns[i];
/* Low row value */
int j_low = t->rows[j];
/* Interpolation results for the upper and lower rows */
int o0, o1;
/* Prevent division by zero if the input values aren't increasing.
If no division by zero, interpolate between columns in the upper and
lower row. */
if (i_delta == 0)
{
o0 = row0[i];
o1 = row1[i];
is_fault = true;
}
else
{
/* Interpolate the upper row */
{
int o_low = row0[i]; /* Row value at low column # */
int o_delta = row0[i + 1] - row0[i]; /* Difference from next column */
o0 = o_low + ((ix - i_low) * (long)o_delta) / i_delta;
}
/* Interpolate the lower (higher subscript) row */
{
int o_low = row1[i]; /* Row value at low column # */
int o_delta = row1[i + 1] - row1[i]; /* Difference from next column */
o1 = o_low + ((ix - i_low) * (long)o_delta) / i_delta;
}
}
/* Guard against division by zero in the row axis. If all is well,
interpolate between the two row interpolation results from earlier. */
if (j_delta == 0)
{
*o = o0;
is_fault = true;
}
else
{
*o = o0 + ((iy - j_low) * (long)(o1 - o0)) / j_delta;
}
}
return is_fault;
}
/* Header file */
#if !defined(_LOOKUP_H)
#define _LOOKUP_H
/**
* @file
* Table lookup with interpolation (1-D and 2-D) header file.
*/
#include <stdbool.h>
/** One dimensional lookup table. */
typedef const struct
{
/** Number of elements in the table. This must be at least 2. */
unsigned char ncols;
/** List of input values. */
int *columns;
/** Table data (output values). The output values list must have the same
length as the input list. */
int *table;
} Table1d;
/** Two dimensional lookup table. */
typedef const struct
{
/** Number of columns (X values) in the table. Must be at least 2. */
unsigned char ncols;
/** Number of rows (Y values) in the table. Must be at least 2. */
unsigned char nrows;
/** X-axis input values list. */
int *columns;
/** Y-axis input values list. */
int *rows;
/** Table data. This is an array of <code>columns</code>X<code>rows</code>,
arranged in rows. For example, <code>table[1]</code> is the second
column in the first row. */
int *table;
} Table2d;
/* Prototypes */
bool lookup1d (Table1d *t, int ix, int *o);
bool lookup2d (Table2d *t, int ix, int iy, int *o);
#endifDelay for MSP430
void configureClocks();
void delay_ms(unsigned int ms);
void delay_us(unsigned int us);
void configureClocks()
{
WDTCTL = WDTPW + WDTHOLD; // Stop WDT
BCSCTL1 = CALBC1_1MHZ;
DCOCTL = CALDCO_1MHZ;
}
void delay_us(unsigned int us)
{
while (us)
{
__delay_cycles(1); // 1 for 1 Mhz set 16 for 16 MHz
us--;
}
}
void delay_ms(unsigned int ms)
{
while (ms)
{
__delay_cycles(1000); 1000 for 1MHz and 16000 for 16MHz
ms--;
}
}Additive White Gaussian Noise Generator
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define PI 3.1415926536
double AWGN_generator()
{/* Generates additive white Gaussian Noise samples with zero mean and a standard deviation of 1. */
double temp1;
double temp2;
double result;
int p;
p = 1;
while( p > 0 )
{
temp2 = ( rand() / ( (double)RAND_MAX ) ); /* rand() function generates an
integer between 0 and RAND_MAX,
which is defined in stdlib.h.
*/
if ( temp2 == 0 )
{// temp2 is >= (RAND_MAX / 2)
p = 1;
}// end if
else
{// temp2 is < (RAND_MAX / 2)
p = -1;
}// end else
}// end while()
temp1 = cos( ( 2.0 * (double)PI ) * rand() / ( (double)RAND_MAX ) );
result = sqrt( -2.0 * log( temp2 ) ) * temp1;
return result; // return the generated random sample to the caller
}// end AWGN_generator()Macros to get and set a bit field within a value
// Get a bit field from a value
#define GetField(Var, Mask, Shift) \
(((Var) >> (Shift)) & (Mask))
// Set a bit field in a value
#define SetField(Var, Mask, Shift, Val) \
(Var) = (((Var) & ~((Mask) << (Shift))) | (((Val) & (Mask)) << (Shift)))Fast non-754 floating point library for Freescale 56F800E series
#ifndef ALREADY_READ_FFLOATV2A_H
#define ALREADY_READ_FFLOATV2A_H
/*******************************************************************************
FFloat Number Definitions
*******************************************************************************/
#define MINUSONEFF 0x00008000 //FFloat number -1
#define ZEROFF 0xFF800000 //FFloat number 0
#define ONEFF 0x00014000 //FFloat number 1
#define TWOFF 0x00024000 //FFloat number 2
#define THREEFF 0x00026000 //FFloat number 3
#define FOURFF 0x00034000 //FFloat number 4
#define FIVEFF 0x00035000 //FFloat number 5
#define SIXFF 0x00036000 //FFloat number 6
#define SEVENFF 0x00037000 //FFloat number 7
#define EIGHTFF 0x00044000 //FFloat number 8
#define NINEFF 0x00044800 //FFloat number 9
#define TENFF 0x00045000 //FFloat number 10
#define ELEVENFF 0x00045800 //FFloat number 11
#define TWELVEFF 0x00046000 //FFloat number 12
#define NOMINALBATVOLTAGE 0x00044800
/*******************************************************************************
FFloat Data Type Definition
*******************************************************************************/
typedef unsigned char bool;
typedef long unsigned int ffloat;
/*******************************************************************************
FFloat FUNCTION PROTOTYPES
*******************************************************************************/
asm ffloat FFabs(register ffloat ffnum);
asm ffloat FFneg(register ffloat ffnum);
asm ffloat S16int2FFloat(register short int inum);
asm ffloat S32int2FFloat(register long int inum);
asm ffloat U32int2FFloat(register long unsigned int unum);
asm ffloat FFadd(register ffloat ffnum1,register ffloat ffnum2);
asm ffloat FFdiv(register ffloat ffnum1,register ffloat ffnum2);
asm short int FFloatTrunc2S16int(register ffloat ffnum);
asm short int FFloatRnd2S16int(register ffloat ffnum);
asm ffloat FFmult(register ffloat ffnum1,register ffloat ffnum2);
asm ffloat FFsub(register ffloat ffnum1,register ffloat ffnum2);
asm ffloat IEEE2FFloat(register float fnum);
float FFloat2IEEE(ffloat ffnum);
asm bool FFgt(register ffloat ffnum1, register ffloat ffnum2);
asm bool FFlt(register ffloat ffnum1, register ffloat ffnum2);
asm bool FFgte(register ffloat a, register ffloat b);
asm bool FFlte(register ffloat a, register ffloat b);
asm bool FFgtz(register ffloat ffnum);
asm bool FFltz(register ffloat ffnum);
asm bool FFeqz(register ffloat ffnum);
ffloat FFatan(ffloat xin);
ffloat FFsin(ffloat xin);
ffloat FFcos(ffloat xin);
#endif
**********************************************************
Function code begins below
**********************************************************
#include "FFloatV2A.h"
ffloat FFatan(ffloat xin)
{
int k,klo,khi;
ffloat xdiff0, xdiff1;
ffloat x=xin;
static ffloat xlo = 0x0005b000;
static ffloat xhi = 0x00055000;
static ffloat ya[151] = {0x00019eaa, 0x00019eb5, 0x00019ec0, 0x00019ecc, 0x00019ed8, 0x00019ee4, 0x00019ef1, 0x00019efe, 0x00019f0c, 0x00019f19, 0x00019f28, 0x00019f36, 0x00019f46, 0x00019f55, 0x00019f66, 0x00019f76, 0x00019f88, 0x00019f99, 0x00019fac, 0x00019fbf, 0x00019fd3, 0x00019fe8, 0x00019ffd, 0x0001a013, 0x0001a02a, 0x0001a042, 0x0001a05b, 0x0001a075, 0x0001a090, 0x0001a0ac, 0x0001a0ca, 0x0001a0e9, 0x0001a109, 0x0001a12b, 0x0001a14e, 0x0001a173, 0x0001a19a, 0x0001a1c3, 0x0001a1ee, 0x0001a21c, 0x0001a24c, 0x0001a27f, 0x0001a2b5, 0x0001a2ef, 0x0001a32c, 0x0001a36d, 0x0001a3b3, 0x0001a3fd, 0x0001a44d, 0x0001a4a2, 0x0001a4ff, 0x0001a563, 0x0001a5d0, 0x0001a646, 0x0001a6c7, 0x0001a754, 0x0001a7f0, 0x0001a89d, 0x0001a95d, 0x0001aa33, 0x0001ab25, 0x0001ac37, 0x0001ad71, 0x0001aeda, 0x0001b07f, 0x0001b26e, 0x0001b4bc, 0x0001b785, 0x0001baf1, 0x0001bf38, 0x0000894e, 0x00009757, 0x0000a9a2, 0xffff8292, 0xffffbd49, 0xff800000, 0xffff42b6, 0xffff7d6d, 0x0000565d, 0x000068a8, 0x000076b1, 0x000140c7, 0x0001450e, 0x0001487a, 0x00014b43, 0x00014d91, 0x00014f80, 0x00015125, 0x0001528e, 0x000153c8, 0x000154da, 0x000155cc, 0x000156a2, 0x00015762, 0x0001580f, 0x000158ab, 0x00015938, 0x000159b9, 0x00015a2f, 0x00015a9c, 0x00015b00, 0x00015b5d, 0x00015bb2, 0x00015c02, 0x00015c4c, 0x00015c92, 0x00015cd3, 0x00015d10, 0x00015d4a, 0x00015d80, 0x00015db3, 0x00015de3, 0x00015e11, 0x00015e3c, 0x00015e65, 0x00015e8c, 0x00015eb1, 0x00015ed4, 0x00015ef6, 0x00015f16, 0x00015f35, 0x00015f53, 0x00015f6f, 0x00015f8a, 0x00015fa4, 0x00015fbd, 0x00015fd5, 0x00015fec, 0x00016002, 0x00016017, 0x0001602c, 0x00016040, 0x00016053, 0x00016066, 0x00016077, 0x00016089, 0x00016099, 0x000160aa, 0x000160b9, 0x000160c9, 0x000160d7, 0x000160e6, 0x000160f3, 0x00016101, 0x0001610e, 0x0001611b, 0x00016127, 0x00016133, 0x0001613f, 0x0001614a, 0x00016155};
static ffloat y2a[151] = {0xff800000, 0xfff443e4, 0xfff446b6, 0xfff449b0, 0xfff44cd5, 0xfff45029, 0xfff453af, 0xfff4576a, 0xfff45b5f, 0xfff45f92, 0xfff46408, 0xfff468c6, 0xfff46dd1, 0xfff47331, 0xfff478ec, 0xfff47f0a, 0xfff542c9, 0xfff54648, 0xfff54a06, 0xfff54e0a, 0xfff55259, 0xfff556fa, 0xfff55bf6, 0xfff56156, 0xfff56722, 0xfff56d66, 0xfff5742f, 0xfff57b8a, 0xfff641c3, 0xfff6461c, 0xfff64ad8, 0xfff65004, 0xfff655ac, 0xfff65be0, 0xfff662b0, 0xfff66a30, 0xfff67278, 0xfff67ba1, 0xfff742e5, 0xfff7488b, 0xfff74ed9, 0xfff755e6, 0xfff75dd0, 0xfff766ba, 0xfff770cc, 0xfff77c39, 0xfff8449e, 0xfff84c0f, 0xfff8549c, 0xfff85e7b, 0xfff869ef, 0xfff8774e, 0xfff9437f, 0xfff94cc5, 0xfff957cc, 0xfff96504, 0xfff974fc, 0xfffa4439, 0xfffa5032, 0xfffa5f16, 0xfffa71cd, 0xfffb44d0, 0xfffb542e, 0xfffb684a, 0xfffc4182, 0xfffc538f, 0xfffc6c5c, 0xfffd4779, 0xfffd5fe2, 0xfffe4133, 0xfffe5918, 0xfffe77b6, 0xffff4b62, 0xffff503a, 0xfffe707d, 0xff800000, 0xfffe8f82, 0xffffafc5, 0xffffb49d, 0xfffe8849, 0xfffea6e7, 0xfffebecc, 0xfffda01d, 0xfffdb886, 0xfffc93a3, 0xfffcac70, 0xfffcbe7d, 0xfffb97b5, 0xfffbabd1, 0xfffbbb2f, 0xfffa8e32, 0xfffaa0e9, 0xfffaafcd, 0xfffabbc6, 0xfff98b03, 0xfff99afb, 0xfff9a833, 0xfff9b33a, 0xfff9bc80, 0xfff888b1, 0xfff89610, 0xfff8a184, 0xfff8ab63, 0xfff8b3f0, 0xfff8bb61, 0xfff783c6, 0xfff78f33, 0xfff79945, 0xfff7a22f, 0xfff7aa19, 0xfff7b126, 0xfff7b774, 0xfff7bd1a, 0xfff6845e, 0xfff68d87, 0xfff695cf, 0xfff69d4f, 0xfff6a41f, 0xfff6aa53, 0xfff6affb, 0xfff6b527, 0xfff6b9e3, 0xfff6be3c, 0xfff58475, 0xfff58bd0, 0xfff59299, 0xfff598dd, 0xfff59ea9, 0xfff5a409, 0xfff5a905, 0xfff5ada6, 0xfff5b1f5, 0xfff5b5f9, 0xfff5b9b7, 0xfff5bd36, 0xfff480f5, 0xfff48713, 0xfff48cce, 0xfff4922e, 0xfff49739, 0xfff49bf7, 0xfff4a06d, 0xfff4a4a0, 0xfff4a895, 0xfff4ac50, 0xfff4afd6, 0xfff4b32a, 0xfff4b64f, 0xfff4b949, 0xfff4bc1b, 0xfff4bc1b};
static int numpoints = 151;
static ffloat h = 0xffff4444;
static ffloat hinv = 0x00027800;
klo = FFloatTrunc2S16int(FFmult(FFsub(x,xlo),hinv));
khi=klo+1;
if(FFlt(x,xlo)){
return(ya[0]);
}else if(FFgt(x,xhi)){
return(ya[numpoints-1]);
}
xdiff0 = FFsub(x, FFadd(xlo, FFmult(h,S16int2FFloat(klo))));
xdiff1 = FFsub(xdiff0, h);
return ( FFadd(ya[klo], FFadd(FFmult(FFmult(FFsub(ya[khi],ya[klo]), hinv), xdiff0), FFmult(FFmult(y2a[khi], xdiff0), xdiff1))) );
}
ffloat FFcos(ffloat xin)
{
int k,klo,khi;
ffloat xdiff0, xdiff1;
ffloat x=xin;
static ffloat xlo = 0x00029b78;
static ffloat xhi = 0x00026487;
static ffloat ya[31] = {0x00008000, 0x000082cc, 0x00008b10, 0x00009872, 0x0000aa59, 0xffff8000, 0xffffb0e4, 0xfffd94f6, 0xfffd6b09, 0xffff4f1b, 0x00004000, 0x000055a6, 0x0000678d, 0x000074ef, 0x00007d33, 0x00014000, 0x00007d33, 0x000074ef, 0x0000678d, 0x000055a6, 0x00004000, 0xffff4f1b, 0xfffd6b09, 0xfffd94f6, 0xffffb0e4, 0xffff8000, 0x0000aa59, 0x00009872, 0x00008b10, 0x000082cc, 0x00008000};
static ffloat y2a[31] = {0xff800000, 0xffff7cbe, 0xffff7481, 0xffff672d, 0xffff5556, 0xfffe7f88, 0xfffe4ed1, 0xfffc6aa5, 0xfffc955a, 0xfffeb12e, 0xfffe8077, 0xffffaaa9, 0xffff98d2, 0xffff8b7e, 0xffff8341, 0xffff8077, 0xffff8341, 0xffff8b7e, 0xffff98d2, 0xffffaaa9, 0xfffe8077, 0xfffeb12e, 0xfffc955a, 0xfffc6aa5, 0xfffe4ed1, 0xfffe7f88, 0xffff5556, 0xffff672d, 0xffff7481, 0xffff7cbe, 0xffff7cbe};
static int numpoints = 31;
static ffloat h = 0xfffe6b3b;
static ffloat hinv = 0x00034c64;
static ffloat pi2=0x00036487;
static ffloat pi2inv=0xfffe517c;
if(FFlt(xin,xlo)){
x=FFadd(
xin,
FFmult(
S16int2FFloat(
FFloatTrunc2S16int(
FFmult(
FFsub(xhi,xin),
pi2inv
)
)
),
pi2
)
);
}else if(FFgt(xin,xhi)){
x=FFsub(
xin,
FFmult(
S16int2FFloat(
FFloatTrunc2S16int(
FFmult(
FFsub(xin,xlo),
pi2inv
)
)
),
pi2
)
);
}
klo = FFloatTrunc2S16int(FFmult(FFsub(x,xlo),hinv));
khi=klo+1;
xdiff0 = FFsub(x, FFadd(xlo, FFmult(h,S16int2FFloat(klo))));
xdiff1 = FFsub(xdiff0, h);
return ( FFadd(ya[klo], FFadd(FFmult(FFmult(FFsub(ya[khi],ya[klo]), hinv), xdiff0), FFmult(FFmult(y2a[khi], xdiff0), xdiff1))) );
}
//Return the negative of ffnum
asm ffloat FFneg(register ffloat ffnum)
{
move.w A1,Y0 //store ffnum exp in Y0
move.w A0,A //A holds mantissa of ffnum
neg A //full 36-bit negate
asr A //shift right to prevent overflow of clb
jeq Zero //Don't normalize if zero
//ffnum != 0
clb A,X0 //Count sign bits
asll.l X0,A //Normalize
sub X0,Y0 //Adjust exponent
inc.w Y0 //Return to normal scale
clb Y0,X0 //check number of sign bits in exponent
cmp.w #8,X0 //If less than 8 (exp > 8 bits),
jlt Exp_Err //jump to exponent exception handler
Continue:
rtsd //delayed return from subroutine
move.w A1,A0 //Move mantissa of sum to lower word of ffnum1 (return value)
move.w Y0,A1 //Move exponent to upper word of ffnum1 (return value)
sxt.l A //Sign-extend A to 36 bits
//end of main neg function
Zero:
rtsd //Delayed return from subroutine - will execute next three words
move.w #$FF80,A //Set exp of sum to minimum
clr.w A0 //Set mantissa of sum to 0
//end of zero handler
Exp_Err:
cmp.w #$007F,Y0
jle Underflow //If not overflow, go to underflow check
tst.w A1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$7FFF,A0 //Max out mantissa
nop //Delay slot filler
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three cycles
move.w #$8000,A0 //Most negative mantissa
nop //Delay slot filler
//end
Underflow:
cmp.w #$FF80,Y0 //Check for underflow
jge Continue //Not an error
tst.w A1 //Positive or negative underflow?
jlt NegU //If negative, go to negative handler
move.w #$FF80,A //Minimum exponent
rtsd
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //filler for third delay slot
//end of E_Err
}
//Return the absolute value of ffnum
asm ffloat FFabs(register ffloat ffnum)
{
move.w A1,Y0 //store ffnum exp in Y0
move.w A0,A //A holds mantissa of ffnum
abs A //full-width absolute value
asr A //shift right to prevent overflow of clb
jeq Zero //Don't normalize if zero
//ffnum != 0
clb A,X0 //Count sign bits
asll.l X0,A //Normalize
sub X0,Y0 //Adjust exponent
inc.w Y0 //Return to normal scale
clb Y0,X0 //check number of sign bits in exponent
cmp.w #8,X0 //If less than 8 (exp > 8 bits),
jlt Exp_Err //jump to exponent exception handler
Continue:
rtsd //delayed return from subroutine
move.w A,A0 //Move mantissa of sum to lower word of ffnum1 (return value)
move.w Y0,A1 //Move exponent to upper word of ffnum1 (return value)
sxt.l A //Sign-extend A to 36 bits
//end of main abs function
Zero:
rtsd //Delayed return from subroutine - will execute next three words
move.w #$FF80,A //Set exp of sum to minimum
clr.w A0 //Set mantissa of sum to 0
//end of zero handler
Exp_Err:
cmp.w #$007F,Y0
jle Underflow //If not overflow, go to underflow check
tst.w A1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$7FFF,A0 //Max out mantissa
nop //Delay slot filler
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three cycles
move.w #$8000,A0 //Most negative mantissa
nop //Delay slot filler
//end
Underflow:
cmp.w #$FF80,Y0 //Check for underflow
jge Continue //Not an error
tst.w A1 //Positive or negative underflow?
jlt NegU //If negative, go to negative handler
move.w #$FF80,A //Minimum exponent
rtsd
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //filler for third delay slot
//end of E_Err
}
//convert an int16 to an ffloat value
asm ffloat S16int2FFloat(register short int inum)
{
tst.w Y0
jeq Zero
//inum != 0
clb Y0,X0
asll.l X0,Y0 //normalize inum
neg X0 //set exponent
rtsd
add.w #15,X0
move.w X0,A //exponent
move.w Y0,A0 //mantissa
//FFloat zero = 0xFF800000
Zero:
rtsd
move.w #$FF80,A
clr.w A0
}
asm ffloat FFadd(register ffloat ffnum1,register ffloat ffnum2)
{
move.w A0,X0 //Store ffnum1 mantissa temporarily in X0
move.w B0,Y0 //Store ffnum2 mantissa temporarily in Y0
move.w A1,Y1 //Put ffnum1 exponent (exp1) in Y1
sub B,Y1 //Y1 = exp1 - exp2
//Setup: Larger ffnum exponent goes in Y0; mantissa to be shifted goes in B1;
//mantissa to stay the same goes in A1; abs exp difference goes in Y1
tlt B,A //Move ffnum2 (mantissa and exp) to A (not shifted) if Y1 neg
tlt X0,B //Move ffnum1 mantissa to B1 for shifting if Y1 neg
tge Y0,B //Move ffnum2 mantissa to B1 for shifting if Y1 not negative
abs Y1 //positive shift values
cmp.w #15,Y1 //More than 15-bit shift (ASRAC only works to 15 bits)?
jgt Neglect //If yes, an input ffnum will go to zero if shifted
move.w A1,Y0 //Move larger exp to Y0 for shifting
move.w A0,A //Move mantissa A0 to A1 for adding
asrac B1,Y1,A //Extend B1 to 36 bits, shift right by Y1, and add to A
asr A //Shift right to prevent overflow of CLB (next)
clb A,X0 //Count sign bits
asll.l X0,A //Normalize
tst.w A1 //Check if relevant part of result is zero
jeq Zero //Result is zero
sub X0,Y0 //Adjust exponent of exp1
inc.w Y0 //Return to normal scale
clb Y0,X0 //check number of sign bits in exponent
cmp.w #8,X0 //If less than 8 (exp > 8 bits),
jlt Exp_Err //jump to exponent exception handler
Continue:
rnd A //round to 16 bits in A1
rtsd //delayed return from subroutine
move.w A,A0 //Move mantissa of sum to lower word of ffnum1 (return value)
move.w Y0,A1 //Move exponent to upper word of ffnum1 (return value)
sxt.l A //Sign-extend A to 36 bits
//end of main add function
Zero:
rtsd //Delayed return from subroutine - will execute next three words
move.w #$FF80,A //Set exp of sum to minimum
clr.w A0 //Set mantissa of sum to 0
//end of zero handler
Exp_Err:
cmp.w #$007F,Y0
jle Underflow //If not overflow, go to underflow check
tst.w A1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$7FFF,A0 //Max out mantissa
nop //Delay slot filler
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three cycles
move.w #$8000,A0 //Most negative mantissa
nop //Delay slot filler
//end
Underflow:
cmp.w #$FF80,Y0 //Check for underflow
jge Continue //Not an error
tst.w A1 //Positive or negative underflow?
jlt NegU //If negative, go to negative handler
move.w #$FF80,A //Minimum exponent
rtsd
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //filler for third delay slot
//end of E_Err
Neglect:
rts //The input with the larger exp becomes the output
}
asm ffloat FFdiv(register ffloat ffnum1, register ffloat ffnum2)
{
move.w A1,X0 //Move exponent of ffnum1 to X0
move.w B1,Y0 //Move exponent of ffnum2 to Y0
move.w A0,Y1 //Move mantissa of ffnum1 to Y1 for sign check
move.w A0,A //Move mantissa of ffnum1 to A1
move.w B0,B //Move mantissa of ffnum2 to B1
eor.w B,Y1 //Calculate sign of final result
//(sign bit of result will be 1=negative if inputs signs differ)
abs A
abs B
jeq DivZero //ffnum2 cannot be zero
L1:
cmp A,B //Check result of B - A
bgt L2 //Ready to divide
brad L1 //Recheck (delayed branch)
asr A //Reduce ffnum1 mantissa by factor of 2
inc.w X0 //Increase ffnum1 exponent by one
//end
L2:
//Division of Positive Fractional Data (A1:A0 / B1)
BFCLR #$0001,SR //Clear carry bit: required for 1st DIV instruction
//REP #16
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
DIV B1,A //Form positive quotient in A0
move.w A0,A //Move A0 to A1
tst.w Y1 //Check sign needed for final result
BGE L3 //Branch if final sign is non-neg
NEG A //Negate mantissa if result is neg
L3:
clb A,Y1 //Count sign bits
asll.l Y1,A //Normalize
tst A //Check if relevant part of result is zero
jeq Zero //Result is zero
sub Y0,X0 //Adjust exponent of exp1
sub Y1,X0
clb X0,Y0 //check size of exponent word
cmp.w #8,Y0
jlt Exp_Err
Continue:
RTSD
MOVE.W A,A0
MOVE.W X0,A1
sxt.l A //Sign-extend A to 36 bits
//END
DivZero:
//Call error handler here
MOVE.W #$007F,A //Needs work here
RTSD
MOVE.W #$7FFF,A0
NOP
//END
Zero:
RTSD
MOVE.W #$FF80,A
CLR.W A0
//END
Exp_Err:
cmp.w #$007F,X0
jle Underflow //If not overflow, go to underflow check
tst.w A1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$7FFF,A0 //Max out mantissa
nop
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$8000,A0 //Most negative mantissa
nop //filler for third delay slot
//end
Underflow:
cmp.w #$FF80,X0 //Check for underflow
jge Continue //Not an error
tst.w A1 //Positive or negative underflow?
jlt NegU //If negative, go to negative handler
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //filler for third delay slot
//end of E_Err
}
asm short int FFloatRnd2S16int(register ffloat ffnum)
{
move.w A1,Y0
move.w A0,A
//Scale so that exponent = 15; converts mantissa to integer scale
//Check if resulting mantissa is in range -32768 to 32767 (16 bit signed int)
sub.w #15,Y0
jgt Over //Number is outside range -32768 to 32767
cmp.w #-17,Y0
jlt Zero //Number is small and rounds to zero
rtsd
asll.l Y0,A //Scale to exponent = 15 (one word, two cycles)
rnd A //Convergent rounding (round down boundary case if even)
move.w A1,Y0
//end
Zero:
rtsd
clr.w Y0 //Result is zero
nop
nop
//end
Over:
tst A
blt Neg //branch to Neg: if number is below -32768
rtsd
move.w #$7FFF,Y0 //Set to most positive 16-bit value
nop //Filler for third delay slot
//end
Neg:
rtsd
move.w #$8000,Y0 //Set to most negative 16-bit value
nop //Filler for third delay slot
//end
}
asm short int FFloatTrunc2S16int(register ffloat ffnum)
{
move.w A1,Y0
move.w A0,A
//Scale so that exponent = 15; converts mantissa to integer scale
//Check if resulting mantissa is in range -32768 to 32767 (16 bit signed int)
sub.w #15,Y0
jgt Over //Number is outside range -32768 to 32767
cmp.w #-17,Y0
jlt Zero //Number is small and rounds to zero
rtsd
asll.l Y0,A //Scale to exponent = 15 (one word, two cycles)
move.w A1,Y0
nop //Filler for third delay slot
//end
Zero:
rtsd
clr.w Y0 //Result is zero
nop
nop
//end
Over:
tst A
blt Neg //branch to Neg: if number is below -32768
rtsd
move.w #$7FFF,Y0 //Set to most positive 16-bit value
nop //Filler for third delay slot
//end
Neg:
rtsd
move.w #$8000,Y0 //Set to most negative 16-bit value
nop //Filler for third delay slot
//end
}
//convert an unsigned int32 to an ffloat value
asm ffloat U32int2FFloat(register long unsigned int unum)
{
tst.l A
jeq Zero //unum = 0
jlt LongUnsigned //If 2^31 <= unum <= 2^32-1, unum will
//be a negative number
//unum <= 2^31 - 1
clb A,X0
asll.l X0,A //normalize unum
neg X0 //set exponent
add.w #31,X0
rtsd
move.w A1,A0 //mantissa
move.w X0,A1 //exponent
sxt.l A //sign-extend A to 36 bits
//FFloat zero = 0xFF800000
Zero:
rtsd
move.w #$FF80,A
clr.w A0
//If unum is between 2^31 and 2^32-1
LongUnsigned:
lsr.w A //divide mantissa by 2
move.w A1,A0 //move mantissa to its right place
//divide the mantissa by two and increase the exponent by 1
//this will correct the sign of A while keeping the absolute
//value of a the same
rtsd
move.w #32,A1 //exponent will always be 32 for this case
sxt.l A //sign-extend A to 36 bits
}
//convert an int32 to an ffloat value
asm ffloat S32int2FFloat(register long int inum)
{
//inum = 0
tst.l A
jeq Zero
//inum != 0
clb A,X0
asll.l X0,A //normalize inum
neg X0 //set exponent
add.w #31,X0
rtsd
move.w A1,A0 //mantissa
move.w X0,A1 //exponent
sxt.l A //sign-extend A to 36 bits
//FFloat zero = 0xFF800000
Zero:
rtsd
move.w #$FF80,A
clr.w A0
}
//typedef long unsigned int ffloat;
asm ffloat FFmult(register ffloat ffnum1, register ffloat ffnum2)
{
move.w B1,Y1 //This is to save exp2, use B for mult, and prepare for exp add
move.w A0,X0 //Can't multiply A0,B0 directly
move.w B0,Y0
mpyr X0,Y0,B //Multiply with round; result unlikely to differ from mpy, since truncated later
asr B //Shift right, so CLB can give correct count
clb B,X0 //Count sign bits for normalization
asll.l X0,B //Normalize
tst.w B1 //Check if relevant part of result is zero
jeq Zero //Go to zero handler
add A,Y1 //add A1 to Y1
sub X0,Y1 //Update exponent after normalization
inc.w Y1 //Return to normal scale
clb Y1,Y0 //count sign bits in exponent word
cmp.w #8,Y0 //If <8 (exp > 8 bits),
jlt Exp_Err //jump to exponent exception handler
Continue:
rtsd //return with 3-cyle delay
move.w Y1,A //Put exp in return register
rnd B //Round to 16 bits in B1
move.w B1,A0 //Move mantissa to A0
//end of mult routine
Zero:
rtsd //return with 3-cyle delay
move.w #$FF80,A //Set exp of sum to minimum
clr.w A0 //Set mantissa of sum to 0
//end of zero handler
Exp_Err:
cmp.w #$007F,Y1 //Check for overflow
jle Underflow //If not overflow, go to underflow check
tst.w B1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$7FFF,A0 //Max out mantissa
rtsd //Delayed return - will execute next three words
nop //Filler for third delay slot
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return - will execute next three words
move.w #$8000,A0 //Most negative mantissa
nop //Filler for third delay slot
//end
Underflow:
cmp.w #$FF80,Y1 //Check for underflow
jge Continue //Not an error - continue normal code
tst.w B1 //Positive or negative overflow?
jlt NegU //If negative, go to negative handler
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return - will execute next three words
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return - will execute next three words
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //Filler for third delay slot
//end of Exp_Err
}
asm ffloat FFsub(register ffloat ffnum1,register ffloat ffnum2)
{
move.w A0,X0 //Store ffnum1 mantissa temporarily in X0
move.w B1,Y1 //Store ffnum2 mantissa temporarily in Y1
move.w B0,B //Prepare to negate B
asr B //Prevent overflow
inc.w Y1 //Adjust exponent
neg B //Negate
clb B,Y0 //Count leading bits
asll.l Y0,B //rescale
sub Y0,Y1 //adjust exponent
move.w B1,Y0
move.w Y1,B
move.w Y0,B0
move.w A1,Y1 //Put ffnum1 exponent (exp1) in Y1
sub B,Y1 //Y1 = exp1 - exp2
//Setup: Larger ffnum exponent goes in Y0; mantissa to be shifted goes in B1;
//mantissa to stay the same goes in A1; abs exp difference goes in Y1
tlt B,A //Move ffnum2 (mantissa and exp) to A (not shifted) if Y1 neg
tlt X0,B //Move ffnum1 mantissa to B1 for shifting if Y1 neg
tge Y0,B //Move ffnum2 mantissa to B1 for shifting if Y1 not negative
abs Y1 //positive shift values
cmp.w #15,Y1 //More than 15-bit shift (ASRAC only works to 15 bits)?
jgt Neglect //If yes, an input ffnum will go to zero if shifted
move.w A1,Y0 //Move larger exp to Y0 for shifting
move.w A0,A //Move mantissa A0 to A1 for adding
asrac B1,Y1,A //Extend B1 to 36 bits, shift right by Y1, and add to A
asr A //Shift right to prevent overflow of CLB (next)
clb A,X0 //Count sign bits
asll.l X0,A //Normalize
tst.w A1 //Check if relevant part of result is zero
jeq Zero //Result is zero
sub X0,Y0 //Adjust exponent of exp1
inc.w Y0 //Return to normal scale
clb Y0,X0 //check size of exponent word
cmp.w #8,X0
jlt Exp_Err
Continue:
rnd A //Round to 16 bits
rtsd //delayed return from subroutine
move.w A,A0 //Move mantissa of sum to lower word of ffnum1 (return value)
move.w Y0,A1 //Move exponent to upper word of ffnum1 (return value)
sxt.l A //Sign-extend A to 36 bits
//end of main add function
Zero:
rtsd //Delayed return from subroutine - will execute next three inst.
move.w #$FF80,A //Set exp of sum to minimum
clr.w A0 //Set mantissa of sum to 0
//end of zero handler
Exp_Err:
cmp.w #$007F,Y0
jle Underflow //If not overflow, go to underflow check
tst.w A1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$7FFF,A0 //Max out mantissa
nop //filler for third delay slot
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$8000,A0 //Most negative mantissa
nop //filler for third delay slot
//end
Underflow:
cmp.w #$FF80,Y0 //Check for underflow
jge Continue //Not an error
tst.w A1 //Positive or negative underflow?
jlt NegU //If negative, go to negative handler
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three inst.
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three inst.
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //filler for third delay slot
//end of E_Err
Neglect:
rts //The input with the larger exp becomes the output
}
asm ffloat IEEE2FFloat(register float fnum)
{
bftstl #$7F80,A1
jcs Zero //For IEEE, zero is indicated by zero exp.
move.w A1,Y0
bfclr #$FF00,A1
sxt.l A //Sign-extend A to 36 bits
bfset #$0080,A1
brclr #$8000,Y0,L1 //Branch if sign bit is positive
neg A //Negate mantissa if sign bit is negative
L1:
clb A,X0 //Normalize mantissa
asll.l X0,A
bfclr #$807F,Y0
lsrr.w #7,Y0
sub.w #119,Y0
sub X0,Y0 //FFloat exponent is ready
clb Y0,X0 //Check for overflow/underflow
cmp.w #8,X0
jlt Exp_Err
Continue:
rnd A
rtsd
move.w A,A0
move.w Y0,A1
sxt.l A //Sign-extend A to 36 bits
//end
Zero:
RTSD
MOVE.W #$FF80,A
CLR.W A0
//END
Exp_Err:
cmp.w #$007F,Y0
jle Underflow //If not overflow, go to underflow check
tst.w A1 //Positive or negative overflow?
jlt NegO //If negative, go to negative handler
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$7FFF,A0 //Max out mantissa
nop //filler for third delay slot
//end
NegO:
move.w #$007F,A //Max out exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$8000,A0 //Most negative mantissa
nop //filler for third delay slot
//end
Underflow:
cmp.w #$FF80,Y0 //Check for underflow
jge Continue //Not an error
tst.w A1 //Positive or negative underflow?
jlt NegU
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$4000,A0 //Minimum normalized positive mantissa
nop //Filler for third delay slot
//end
NegU:
move.w #$FF80,A //Minimum exponent
rtsd //Delayed return from subroutine - will execute next three words
move.w #$BFFF,A0 //Minimum (abs) normalized negative mantissa
nop //filler for third delay slot
//end of E_Err
}
//A not very good C function. Ok for testing other functions in simulation.
//Converts an FFloat number to an IEEE 754-compatible single precision floating point number.
//typedef long unsigned int ffloat;
float FFloat2IEEE(ffloat ffnum)
{
float fout = 0;
long int iexp = 0;
long unsigned int tempout = 0, sign = 0, mantissa = 0, exp = 0;
void *VoidPointer;
float *FloatPointer;
long unsigned int *LintPointer;
if (ffnum&0xFFFF) //ffnum is not zero
{
mantissa = ffnum & 0x0000FFFF;
exp = ffnum&0xFFFF0000;
iexp = (long int)exp;
iexp += 0x007F0000; //Bias exponent positive by 127
if (iexp < 0x00010000) //Limit exponent size to allowed IEEE range
{
iexp = 0x00010000;
}
else if (iexp > 0x00FE0000)
{
iexp = 0x00FE0000;
}
if (mantissa&0x00008000) //ffnum is negative
{
sign = 0x80000000;
mantissa ^= 0x0000FFFF; //Negate
mantissa++;
}
while (!(mantissa&0x8000)) //normalize
{
mantissa <<= 1;
iexp -= 0x00010000;
}
if (iexp < 0x00010000) //Limit exponent size to allowed IEEE range
{
iexp = 0x00010000;
}
else if (iexp > 0x00FE0000)
{
iexp = 0x00FE0000;
}
exp = (long unsigned int)iexp;
exp <<= 7; //Shift exponent to correct position
mantissa <<= 8; //Shift to correct IEEE position
mantissa &= 0x007FFFFF; //Clear leading one
tempout = sign | exp | mantissa;
}
else exp = 0x00000000; //zero
VoidPointer = &(tempout); //obtain pointer to unsigned long int tempout
FloatPointer = VoidPointer; //convert to float
fout = *FloatPointer;
return(fout);
}
//return true if ffnum1>ffnum2, false otherwise
asm bool FFgt(register ffloat ffnum1, register ffloat ffnum2)
{
//First compare signs of numbers
tst.w A0
blt CheckSignANeg
//a is nonnegative
tst.w B0
//Both numbers are nonnegative - nonnegative exponents case
bge CasePNumExp
//If b is negative, a>b
rtsd
move.w #1,Y0
nop
nop
//a is negative
CheckSignANeg:
tst.w B0
//Both numbers are negative - negative exponents case
blt CaseNNumExp
//If b is nonnegative, a<b
rtsd
move.w #0,Y0
nop
nop
//If a and b are positive, go here
//larger exponent = larger #
CasePNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
blt aGTb //if(expB<expA) then a>b
bgt aNotGTb //if(expB>expA) then !(a>b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
blt aGTb //if(mantissaB<mantissaA) then a>b
rtsd
move.w #0,Y0
nop
nop
//If a and b are negative, go here
//larger exponent = smaller #
CaseNNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
bgt aGTb //if(expB>expA) then a>b
blt aNotGTb //if(expB<expA) then !(a>b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
blt aGTb //if(mantissaB<mantissaA) then a>b
rtsd
move.w #0,Y0
nop
nop
//if a>b, go here
aGTb:
rtsd
move.w #1,Y0
nop
nop
//if a<=b, go here
aNotGTb:
rtsd
move.w #0,Y0
nop
nop
}
//return true if ffnum>0, false otherwise
asm bool FFgtz(register ffloat ffnum)
{
//Test ffnum mantissa
tst.w A0
bgt Positive
//ffnum <= 0
rtsd //delayed return
clr.w Y0 //return value 0
nop //first filler instruction
nop //second filler instruction
//end
Positive:
//ffnum > 0
rtsd //delayed return
move.w #1,Y0 //return value 1
nop //first filler instruction
nop //second filler instruction
//end
}
//return true if ffnum<0, false otherwise
asm bool FFltz(register ffloat ffnum)
{
//Test ffnum mantissa
tst.w A0
blt Negative
//ffnum >= 0
rtsd //delayed return
clr.w Y0 //return value 0
nop //first filler instruction
nop //second filler instruction
//end
Negative:
//ffnum < 0
rtsd //delayed return
move.w #1,Y0 //return value 1
nop //first filler instruction
nop //second filler instruction
//end
}
//return true if ffnum=0, false otherwise
asm bool FFeqz(register ffloat ffnum)
{
//Test ffnum mantissa
tst.w A0
beq Zero
//ffnum != 0
rtsd //delayed return
clr.w Y0 //return value 0
nop //first filler instruction
nop //second filler instruction
//end
Zero:
//ffnum < 0
rtsd //delayed return
move.w #1,Y0 //return value 1
nop //first filler instruction
nop //second filler instruction
//end
}
//return true if ffnum1<ffnum2, false otherwise
asm bool FFlt(register ffloat ffnum1, register ffloat ffnum2)
{
//First compare signs of numbers
tst.w A0
blt CheckSignANeg
//a is nonnegative
tst.w B0
//Both numbers are nonnegative - nonnegative exponents case
bge CasePNumExp
//If b is negative, !(a<b)
rtsd
move.w #0,Y0
nop
nop
//a is negative
CheckSignANeg:
tst.w B0
//Both numbers are negative - negative exponents case
blt CaseNNumExp
//If b is nonnegative, a<b
rtsd
move.w #1,Y0
nop
nop
//If a and b are positive, go here
//larger exponent = larger #
CasePNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
bgt aLTb //if(expB>expA) then a<b
blt aNotLTb //if(expB<expA) then !(a<b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
bgt aLTb //if(mantissaB>mantissaA) then a<b
rtsd
move.w #0,Y0
nop
nop
//If a and b are negative, go here
//larger exponent = smaller #
CaseNNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
blt aLTb //if(expB<expA) then a<b
bgt aNotLTb //if(expB>expA) then !(a<b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
bgt aLTb //if(mantissaB>mantissaA) then a<b
rtsd
move.w #0,Y0
nop
nop
//if a<b, go here
aLTb:
rtsd
move.w #1,Y0
nop
nop
//if a>=b, go here
aNotLTb:
rtsd
move.w #0,Y0
nop
nop
}
//return true if a>=b, false otherwise
asm bool FFgte(register ffloat a, register ffloat b)
{
//First compare signs of numbers
tst.w A0
blt CheckSignANeg
//a is nonnegative
tst.w B0
//Both numbers are nonnegative - nonnegative exponents case
bge CasePNumExp
//If b is negative, a>=b
rtsd
move.w #1,Y0
nop
nop
//a is negative
CheckSignANeg:
tst.w B0
//Both numbers are negative - negative exponents case
blt CaseNNumExp
//If b is nonnegative, a<b
rtsd
move.w #0,Y0
nop
nop
//If a and b are positive, go here
//larger exponent = larger #
CasePNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
blt aGTEb //if(expB<expA) then a>=b
bgt aNotGTEb //if(expB>expA) then !(a>=b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
ble aGTEb //if(mantissaB<=mantissaA) then a>=b
rtsd
move.w #0,Y0
nop
nop
//If a and b are negative, go here
//larger exponent = smaller #
CaseNNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
bgt aGTEb //if(expB>expA) then a>b
blt aNotGTEb //if(expB<expA) then !(a>b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
ble aGTEb //if(mantissaB<=mantissaA) then a>=b
rtsd
move.w #0,Y0
nop
nop
//if a>=b, go here
aGTEb:
rtsd
move.w #1,Y0
nop
nop
//if a<b, go here
aNotGTEb:
rtsd
move.w #0,Y0
nop
nop
}
//return true if a<=b, false otherwise
asm bool FFlte(register ffloat a, register ffloat b)
{
//First compare signs of numbers
tst.w A0
blt CheckSignANeg
//a is nonnegative
tst.w B0
//Both numbers are nonnegative - nonnegative exponents case
bge CasePNumExp
//If b is negative, !(a<=b)
rtsd
move.w #0,Y0
nop
nop
//a is negative
CheckSignANeg:
tst.w B0
//Both numbers are negative - negative exponents case
blt CaseNNumExp
//If b is nonnegative, a<b
rtsd
move.w #1,Y0
nop
nop
//If a and b are positive, go here
//larger exponent = larger #
CasePNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
bgt aLTEb //if(expB>expA) then a<=b
blt aNotLTEb //if(expB>expA) then !(a<=b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
bge aLTEb //if(mantissaB>=mantissaA) then a>=b
rtsd
move.w #0,Y0
nop
nop
//If a and b are negative, go here
//larger exponent = smaller #
CaseNNumExp:
//move exponent data to X0 and Y0 registers for comparison
move.w A1,X0
move.w B1,Y0
cmp.w X0,Y0
blt aLTEb //if(expB<expA) then a<=b
bgt aNotLTEb //if(expB>expA) then !(a<=b)
//If exponents are equal, check mantissas
move.w A0,X0
move.w B0,Y0
cmp.w X0,Y0
bge aLTEb //if(mantissaB>=mantissaA) then a>=b
rtsd
move.w #0,Y0
nop
nop
//if a<=b, go here
aLTEb:
rtsd
move.w #1,Y0
nop
nop
//if a>b, go here
aNotLTEb:
rtsd
move.w #0,Y0
nop
nop
}
ffloat FFsin(ffloat xin)
{
int k,klo,khi;
ffloat xdiff0, xdiff1;
ffloat x=xin;
static ffloat xlo = 0x00029b78;
static ffloat xhi = 0x00026487;
static ffloat ya[31] = {0xffccb968, 0xfffe958c, 0xffff97e0, 0x0000b4c3, 0x0000a0e0, 0x00009126, 0x00008643, 0x000080b3, 0x000080b3, 0x00008643, 0x00009126, 0x0000a0e0, 0x0000b4c3, 0xffff97e0, 0xfffe958c, 0xff800000, 0xfffe6a73, 0xffff681f, 0x00004b3c, 0x00005f1f, 0x00006ed9, 0x000079bc, 0x00007f4c, 0x00007f4c, 0x000079bc, 0x00006ed9, 0x00005f1f, 0x00004b3c, 0xffff681f, 0xfffe6a73, 0xffcc4698};
static ffloat y2a[31] = {0xff800000, 0xfffd6a0f, 0xfffe67be, 0xffff4af6, 0xffff5ec6, 0xffff6e72, 0xffff794a, 0xffff7ed5, 0xffff7ed5, 0xffff794a, 0xffff6e72, 0xffff5ec6, 0xffff4af6, 0xfffe67be, 0xfffd6a0f, 0xff800000, 0xfffd95f0, 0xfffe9841, 0xffffb509, 0xffffa139, 0xffff918d, 0xffff86b5, 0xffff812a, 0xffff812a, 0xffff86b5, 0xffff918d, 0xffffa139, 0xffffb509, 0xfffe9841, 0xfffd95f0, 0xfffd95f0};
static int numpoints = 31;
static ffloat h = 0xfffe6b3b;
static ffloat hinv = 0x00034c64;
static ffloat pi2=0x00036487;
static ffloat pi2inv=0xfffe517c;
if(FFlt(xin,xlo)){
x=FFadd(
xin,
FFmult(
S16int2FFloat(
FFloatTrunc2S16int(
FFmult(
FFsub(xhi,xin),
pi2inv
)
)
),
pi2
)
);
}else if(FFgt(xin,xhi)){
x=FFsub(
xin,
FFmult(
S16int2FFloat(
FFloatTrunc2S16int(
FFmult(
FFsub(xin,xlo),
pi2inv
)
)
),
pi2
)
);
}
klo = FFloatTrunc2S16int(FFmult(FFsub(x,xlo),hinv));
khi=klo+1;
xdiff0 = FFsub(x, FFadd(xlo, FFmult(h,S16int2FFloat(klo))));
xdiff1 = FFsub(xdiff0, h);
return ( FFadd(ya[klo], FFadd(FFmult(FFmult(FFsub(ya[khi],ya[klo]), hinv), xdiff0), FFmult(FFmult(y2a[khi], xdiff0), xdiff1))) );
}High speed serial and port control for logic analysis
#ifndef TESTPOINTS_H
#define TESTPOINTS_H
#include "gpio.h"
class TpHw
{
public:
//===================================================================================
// TOG, CLR, SET macros provide a means to quickly clear, set or toggle a pin.
// Each macro compiles into a single machine instruction when optimized.
// usage is:
// TOG(AVR32_PIN10);
//===================================================================================
#define TOG(pin) { \
volatile avr32_gpio_port_t *gpio_pin = &AVR32_GPIO.port[pin >> 5]; \
gpio_pin->ovrt = 1 << (pin & 0x1F); }
#define CLR(pin) { \
volatile avr32_gpio_port_t *gpio_pin = &AVR32_GPIO.port[pin >> 5]; \
gpio_pin->ovrc = 1 << (pin & 0x1F); }
#define SET(pin) { \
volatile avr32_gpio_port_t *gpio_pin = &AVR32_GPIO.port[pin >> 5]; \
gpio_pin->ovrs = 1 << (pin & 0x1F); }
//===================================================================================
// TAG provides a means to insert static real time serial data to be displayed on a
// logic analyzer. The TAG macro should be optimized for a baud rate that matches
// the instruction cycle time of the compiler. Each letter compiles into 10
// machine instructions when optimized. Use 8 data bits, no parity and one stop bit.
// usage is:
// TAG(AVR32_PIN10, 'H', 'E', 'L', 'L', 'O');
//===================================================================================
// this macro builds the bit
#define BT(pin, letter, bit) { \
volatile avr32_gpio_port_t *gpio_pin = &AVR32_GPIO.port[pin >> 5]; \
if (letter & bit) \
gpio_pin->ovrs = 1 << (pin & 0x1F); \
else \
gpio_pin->ovrc = 1 << (pin & 0x1F); }
// this macro builds the letter
#define LETTER(pin, letter) { \
BT(pin, letter, 0x00); \
BT(pin, letter, 0x01); \
BT(pin, letter, 0x02); \
BT(pin, letter, 0x04); \
BT(pin, letter, 0x08); \
BT(pin, letter, 0x10); \
BT(pin, letter, 0x20); \
BT(pin, letter, 0x40); \
BT(pin, letter, 0x80); \
BT(pin, 0xff, 0xff); }
// these build the tag
#define LETTER1(pin, letter) LETTER(pin, letter)
#define LETTER2(pin, letter, ...) LETTER1(pin, letter) LETTER1(pin, __VA_ARGS__)
#define LETTER3(pin, letter, ...) LETTER1(pin, letter) LETTER2(pin, __VA_ARGS__)
#define LETTER4(pin, letter, ...) LETTER1(pin, letter) LETTER3(pin, __VA_ARGS__)
#define LETTER5(pin, letter, ...) LETTER1(pin, letter) LETTER4(pin, __VA_ARGS__)
#define LETTER6(pin, letter, ...) LETTER1(pin, letter) LETTER5(pin, __VA_ARGS__)
#define LETTER7(pin, letter, ...) LETTER1(pin, letter) LETTER6(pin, __VA_ARGS__)
#define LETTER8(pin, letter, ...) LETTER1(pin, letter) LETTER7(pin, __VA_ARGS__)
// these calculate the number of arguments passed
#define ARGS_N(x1, x2, x3, x4, x5, x6, x7, x8, N, ...) N
#define RSEQ_N() 8, 7, 6, 5, 4, 3, 2, 1, 0
#define NARG_N(...) ARGS_N(__VA_ARGS__)
#define NARG(...) NARG_N(__VA_ARGS__, RSEQ_N())
// these build the macro to start with (T1 - T8) base on number of arguments
#define PASTE(a, b) a ## b
#define XPASTE(a, b) PASTE(a, b)
#define T_(pin, M_, ...) M_(pin, __VA_ARGS__)
#define TAG(pin, ...) T_(pin, XPASTE(LETTER, NARG(__VA_ARGS__)), __VA_ARGS__)
//=====================================================================================
// textOut provides a means to insert dynamic real time serial data to be displayed
// on a logic analyzer. The code below should be optimized for a baud rate that matches
// the instruction cycle time of the compiler by stuffing no ops where appropriate
// to balance the bit output. Use 8 data bits, no parity and one stop bit. This
// gives a character that should take 55 cycles and doesn't take any time to set up.
// usage is:
// TpHw::textOut(AVR32_PIN_PA22, "HELLO");
//=====================================================================================
static void serialOut(uint32_t pin, uint8_t value)
{
volatile avr32_gpio_port_t *gpio_pin = &AVR32_GPIO.port[pin >> 5];
volatile uint32_t out = 1 << (pin & 0x1F);
// start bit
gpio_pin->ovrc = out;
asm("nop");
// bit 0
if (value & (1 << 0))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 1
if (value & (1 << 1))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 2
if (value & (1 << 2))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 3
if (value & (1 << 3))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 4
if (value & (1 << 4))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 5
if (value & (1 << 5))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 6
if (value & (1 << 6))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// bit 7
if (value & (1 << 7))
{
gpio_pin->ovrs = out;
}
else
{
gpio_pin->ovrc = out;
asm("nop");
}
// stop bit
asm("nop");
asm("nop");
asm("nop");
gpio_pin->ovrs = out;
}
static void textOut(uint32_t pin, char *text)
{
while (*text != 0)
{
serialOut(pin, *text++);
}
}
};
#endifARM Cortex-M Bit Banding
#include <stdint.h>
//! @brief Convert word address + bit position to bitband address.
//!
//! @param address Word address containing of bit
//! @param bit Bit offset (0 = LSB, 31 = MSB)
//! @return Address of bit in bitband region.
volatile uint32_t* getBitBandAddress( volatile void* address, int bit )
{
uint32_t addr = (uint32_t)address ;
uint32_t word_band_base = addr & 0xf0000000 ;
uint32_t bit_band_base = word_band_base | 0x02000000 ;
uint32_t offset = addr - word_band_base ;
return (volatile uint32_t*)(bit_band_base + (offset * 32) + (bit * 4)) ;
}
--- EXAMPLES ---
// Example usage 1: 160 bit array
uint32_t physical_memory[5] = {0} ;
uint32_t* bit_array = getBitBandAddress( physical_memory, 0 ) ;
int bit_array_length = sizeof(physical_memory) * CHAR_BIT ;
for( i = 0; i < bit_array_len; i++ )
{
bit_array[i] = rand() % 2;
}
// Example usage 2: STM32 USART1 Tx Int Enable/Disable
uint32_t* tx_intr_enable_bit_addr = getBitBandAddress( (&(USART1->CR1)), 7 ) ;
*tx_intr_enable_bit_addr = 0 ; // Disable Tx
*tx_intr_enable_bit_addr = 1 ; // Enable Tx
// Example usage 3: C++ reference version of example 2
uint32_t& tx_intr_enable_bit = *getBitBandAddress( (&(USART1->CR1)), 7 ) ;
tx_intr_enable_bit = 0 ; // Disable Tx
tx_intr_enable_bit = 1 ; // Enable TxDebug print trace macro
#if defined NDEBUG
#define TRACE( format, ... )
#else
#define TRACE( format, ... ) printf( "%s::%s(%d) " format, __FILE__, __FUNCTION__, __LINE__, __VA_ARGS__ )
#endif
// Example usage
void example()
{
unsigned var = 0xdeadbeef ;
TRACE( "var=0x%x", var ) ;
}
// Resultant output example:
// example.c::example(5) var=0xdeadbeef
//Macros to get and set a bit field within a value
// Get a bit field from a value
#define GetField(Var, Mask, Shift) \
(((Var) >> (Shift)) & (Mask))
// Set a bit field in a value
#define SetField(Var, Mask, Shift, Val) \
(Var) = (((Var) & ~((Mask) << (Shift))) | (((Val) & (Mask)) << (Shift)))Universal InfraRed remote pass-thru
#define MAX_IR_INDEX 64
#define ESCAPE_COUNT 0x2200ul /* Could be reduced?*/
#pragma udata ircounts
unsigned int lcounts[MAX_IR_INDEX];
unsigned int hcounts[MAX_IR_INDEX];
#pragma interrupt high_isr /*=section(".tmpdata")*/
void high_isr(void) {
unsigned int l;
unsigned int c;
unsigned char th, tl;
l = 0;
TMR1H = 0; // Always write H before L
TMR1L = 0;
// Check that this is the INT0 interrupt
// IRRX is int0
if(INTCONbits.INT0IF)
{
// Disable the interrupt source
INTCONbits.INT0IE = 0;
// the code in the while needs to be balanced so that the ==0 and ==1 bits are the size number of cycles.
while(lindex < MAX_IR_INDEX)
{
while(PORTBbits.RB0 == 0)
{
l++;
if(l == ESCAPE_COUNT)
{
lcounts[lindex] = 0xffff;
goto done;
}
}
tl = TMR1L;
th = TMR1H; // << 8 ;// Always read L before H
lcounts[lindex++] = th * 256 + tl;
l = 0;
TMR1H = 0; // Always right H before L
TMR1L = 0;
while(PORTBbits.RB0 == 1)
{
l++;
if(l == ESCAPE_COUNT)
{
hcounts[hindex] = 0xffff;
goto done;
}
}
tl = TMR1L;
th = TMR1H; //<< 8 ;// Always read L before H
hcounts[hindex++] = th * 256 + tl;
l = 0;
TMR1H = 0; // Always write H before L
TMR1L = 0;
}
}
done:
codeReady = 1;
// reset interrupt status bit
//INTCONbits.INT0IE = 1;
//INTCONbits.INT0IF = 0;
return;
}
void zeroIR() {
unsigned char c;
// Initialize the IR Count holders
lindex = 0;
hindex = 0;
for(c = 0; c < MAX_IR_INDEX; c++)
{
lcounts[c] = 0xdead;
}
codeReady = 0;
// reset interrupt status bit
INTCONbits.INT0IE = 1;
INTCONbits.INT0IF = 0;
}
void transmitIR(void) {
unsigned char c;
// First check that the code is valid by examining the first LCOUNT
// if it is less than our defined threshold we will not transmit it.
// The first lcount holds the low-going preamble, it must be a minimum length or it does not
// represent a valid IR Transmission preamble.
if(lcounts[0] < PREAMBLE_MINIMUM)
{
return;
}
sprintf(serTX, (CAST) "$%c%cIC%d,", id1, id2, lindex);
rs485_puts(serTX);
for(c = 0; c < lindex; c++)
{
sprintf(serTX, (CAST) "%04x,%04x, ", lcounts[c], hcounts[c]);
rs485_puts(serTX);
}
sprintf(serTX, (CAST) "\n");
rs485_puts(serTX);
}Primitive exception processing using macros
#define Try \
jmp_buf ExceptionBuffer; \
int ExceptionStatus = setjmp (ExceptionBuffer); \
if (ExceptionStatus == 0)
#define Catch(Value) else if (ExceptionStatus == (int) (Value))
#define Finally else
#define Throw(Value) \
{ \
int Result = (int) (Value); \
if (Result != 0) { \
longjmp (ExceptionBuffer, Result); \
} \
}
An example using a function to read the OCR register on an SD card:
uint32_t SDCard_OCR (void) {
SDCard_ConfigSSP ( );
Try {
// The card is asked to send its OCR. The OCR is
// placed in module variable mOCRValue by the
// function.
Throw (SDCard_SendCommand (CMD58_READ_OCR));
}
// Error processing.
Catch (SD_TIMEOUT) {
GUI_SendMessage (SDCARD_TIMEOUT);
}
Catch (SD_NO_CARD) {
GUI_SendMessage (SDCARD_NOT_FOUND);
}
Finally { // Unknown SD card error
Throw (SD_NO_CARD); // Rethrow the exception
}
// Executed even if an exception thrown:
SDCard_DeconfigSSP ( );
return mOCRValue; // 0xFFFFFFFF if error
}Simple Bit Manipulation Macros
/* Basic bit manipulation macros
No one should ever have to rewrite these
*/
//Set bit y (0-indexed) of x to '1' by generating a a mask with a '1' in the proper bit location and ORing x with the mask.
#define SET(x,y) x |= (1 << y)
//Set bit y (0-indexed) of x to '0' by generating a mask with a '0' in the y position and 1's elsewhere then ANDing the mask with x.
#define CLEAR(x,y) x &= ~(1<< y)
//Return '1' if the bit value at position y within x is '1' and '0' if it's 0 by ANDing x with a bit mask where the bit in y's position is '1' and '0' elsewhere and comparing it to all 0's. Returns '1' in least significant bit position if the value of the bit is '1', '0' if it was '0'.
#define READ(x,y) ((0u == (x & (1<<y)))?0u:1u)
//Toggle bit y (0-index) of x to the inverse: '0' becomes '1', '1' becomes '0' by XORing x with a bitmask where the bit in position y is '1' and all others are '0'.
#define TOGGLE(x,y) (x ^= (1<<y))Delay for MSP430
void configureClocks();
void delay_ms(unsigned int ms);
void delay_us(unsigned int us);
void configureClocks()
{
WDTCTL = WDTPW + WDTHOLD; // Stop WDT
BCSCTL1 = CALBC1_1MHZ;
DCOCTL = CALDCO_1MHZ;
}
void delay_us(unsigned int us)
{
while (us)
{
__delay_cycles(1); // 1 for 1 Mhz set 16 for 16 MHz
us--;
}
}
void delay_ms(unsigned int ms)
{
while (ms)
{
__delay_cycles(1000); 1000 for 1MHz and 16000 for 16MHz
ms--;
}
}Matlab code to plot values from port in real time
clc
clear all
close all
s1 = serial('COM26', 'BaudRate', 57600);
set(s1,'Terminator',35);
fopen(s1);
V=[];
val='';
time=200;
count=0;
f=0;
% **********************************************************************
% Read Serial values
tic
tt=toc;
while(tt<time)
val=fscanf(s1);
tt=toc;
%########################################################################
A=[];
B=[];
C=[];
b=[];
x=[];
j=1;
if(j<numel(val))
while(val(j)~='$')
a=val(j);
b=[b,a];
j=j+1;
end
A=[A,str2num(b)];
j=j+1;
b=[];
while(val(j)~='*')
a=val(j);
b=[b,a];
j=j+1;
end
B=[B,str2num(b)];
j=j+1;
b=[];
while(val(j)~='#')
a=val(j);
b=[b,a];
j=j+1;
end
C=[C,str2num(b)];
i=j;
b=[];
f=f+i;
end
x=[x,round(toc)];
if(~(isempty(A)&&isempty(B)&&isempty(C)))
subplot(1,2,1)
plot(x,A,'--rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','r','MarkerSize',5);
hold on % if u want this in different graph remove hold on and add "figure" command before each graph;
plot(x,B,'--rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',5);
grid on;
subplot(1,2,2)
plot(x,(B/(A+B))*100,'--rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','m','MarkerSize',5);
hold on
plot(x,C,'--rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5);
grid on;
pause(.01);
end
end
hold off
fclose(s1);PID (Floating Point)
/*! \details This structure holds the data to run a
* floating point PID loop.
*/
typedef struct{
float max /*! \brief Max manipulated value */;
float min /*! \brief Miniumum manipulated value */;
float e /*! \brief Error value */;
float i /*! \brief Integrator value */;
float kp /*! \brief Proportional constant */;
float ki /*! \brief Integrator constant */;
float kd /*! \brief Differential constant */;
} pid_f_t;
/*! \details This function initializes the data in a PID structure.
*
*/
void pid_init_f(pid_f_t * ptr /*! A pointer to the PID data structure */,
float min /*! The manipulated variable's minimum value */,
float max /*! The manipulated variable's maximum value */){
memset(ptr, 0, sizeof(pid_f_t));
ptr->min = min;
ptr->max = max;
}
/*! \details This function updates the value of the manipulated variable (MV)
* based on the current state of the PID loop.
*/
float pid_update_f(float sp /*! The set point */,
float pv /*! The process variable */,
pid_f_t * ptr /*! A pointer to the PID constants */){
float temp;
float e;
float p;
float manp;
float tmpi;
//get the error from the last call
e = ptr->e;
//calculate the new error (set point - present value)
ptr->e = sp - pv;
//use a temp variable for the integrator
tmpi = ptr->i + ptr->e;
//update the manipulated process variable
manp = ptr->kp * ptr->e + ptr->ki * tmpi + ptr->kd * (ptr->e - e);
//the integrator is only updated if the manipulated process is within range
//otherwise the system will likely become unstable
if ( (manp < ptr->max) && (manp > ptr->min) ){
ptr->i = tmpi;
} else if ( manp > ptr->max ){
manp = ptr->max;
} else if ( manp < ptr->min ){
manp = ptr->min;
}
return manp;
}