Important Programming Concepts (Even on Embedded Systems) Part II: Immutability
Other articles in this series:
- Part I: Idempotence
- Part III: Volatility
- Part IV: Singletons
- Part V: State Machines
- Part VI: Abstraction
This article will discuss immutability, and some of its variations in the topic of functional programming.
There are a whole series of benefits to using program variables that… well, that aren’t actually variable, but instead are immutable. The impact of immutability on software design can differ quite a bit, depending on the type of computing platform, and especially whether dynamic memory or concurrent memory access are involved.
When I took my first computer science course in college, the instructors extolled the virtues of immutable data. Here’s the message of the Functional Weenies Wizards: Functions that alter data are flawed and evil, and must be marked (e.g. the exclamation point at the end of set! in Scheme), like the Mark of Cain or the Mark of the Beast; functions that do not alter data are pure and good. I thought they were kind of extreme. (The FW is the guy in the corner at the party who walks up to you and says “Hey, I’ll bet you didn’t realize you’ve been using monads all along!” And when you hear the word “monad”, that’s your cue to run away. Or at least play the Monad Drinking Game and down another shot of Scotch.)
But in the intervening years, I’ve come around a bit to their view, and have become a Functional Wannabe. Yeah, mutability has its place, but there are some real advantages to striving towards immutability, and again, it really depends on the type of programming environment you’re in: if the cost of leaving the input data untouched and returning new output data is high, you’re often stuck with mutable data; otherwise, you really should make data immutable wherever possible.
This assumes you have a choice. Let’s forget for a moment about how you can make your programs use immutable data, and first just focus on the difference.
The Immutable and the Mutable
Consider two pieces of data, the first immutable and the second mutable.
- The text of the Declaration of Independence
- The real-time contents of a stock portfolio, namely an unordered list of stock symbols, each with the number of shares owned.
Here’s what you can do with the Declaration of Independence, and what you can’t do with the stock portfolio:
-
Use copies of it rather than the original. If all we care about is the text, we don’t care whether it’s in one area of memory or another. If there are seven areas of our program that need access to the text of the Declaration of Independence, we don’t care if all seven refer to one chunk of memory, or three of them refer to one chunk and the other four another chunk, or if each has its own copy. With the stock portfolio, if we make a copy, the copy is going to be out of date and will not be updated if there are any changes. Any piece of software that wants access to the stock portfolio must get it from its source.
-
Use the original rather than copies. If no one can change the Declaration of Independence, it’s safe to give out references to it all day. (“Hey bud, wanna see the original copy of the Declaration of Independence? Just go to this bus station locker and look inside; here’s the combination....”) Whereas with the stock portfolio, if we want to give read-only access to other software programs, we have to be paranoid and create a copy, so that we can prevent malicious programs from altering the original.
-
Share access to it without any worry about the problems of concurrency. We can let a thousand different software routines access the text of the Declaration of Independence concurrently. It doesn’t matter. None of them are going to be able to change it, so there’s no risk of data corruption. The stock portfolio is another story. We can let only one software task at a time modify it, and while that modification is taking place, we can’t allow other software tasks to read it.
-
Simplify expressions at compile time. In compiled software, the compiler can precompute the number of words in the Declaration of Independence; we don’t have to execute operations at runtime to compute the number of words. But we can’t count the number of stocks in the portfolio at compile time, because it can change.
-
Cache the result of expressions computed at run-time. We could compute a million different statistics about the Declaration of Independence: the number of times the letter pairs
ou,ha, ortyoccur; the list of words in alphabetical order that score less than 12 points in Scrabble; the complete Markov chain transition matrix of two-letter sequences in the Declaration; the MD5 and SHA1 hashes of the full text; the ROT13 translation of the all the words with at least 10 letters… and so on. We can’t possibly compute them all in advance at compile-time, so it’s not worth doing. But if we do happen to compute some summary statistic once, we can save the results for later, because the Declaration of Independence will never change. We can’t do that with the stock portfolio though. -
Store it in nonvolatile memory. In embedded microcontrollers, the amount of available program memory might be 5 or 10 times larger than the amount of available RAM. This means that RAM is more precious than program memory. We can store the text of the Declaration of Independence in program memory, leaving that precious RAM for something else. The stock portfolio is mutable, so we can’t store it in program memory.
-
Use it as a key in an associative array. Associative arrays are ubiquitous in software. They’re just sets of key-value pairs. Use the key to index a value. There are all sorts of data structures to do so efficiently. The only catch is that the keys have to be immutable (or at least comparable and/or hashable in an immutable way), otherwise we may not be able to find the value again.
Programming Language Support for Immutability
In some programming languages there are keywords that specify a degree of immutability. These are extremely useful, but you should be careful that you know exactly what these keywords mean if you do use them. C/C++ have const and Java has final, but these have different meanings, and neither one marks an object as truly immutable.
In C and C++, the const keyword has several usages. When applied to a program variable or function argument, it means that the code given access to that data is not allowed to change it, within the appropriate scope:
int doofus123(const data_t *mydata, data_t *mydata2)
{
const data_t *mydata3 = mydata2;
...
}
Here the variables mydata and mydata3 are marked as pointers to const data. The code within doofus123() is not allowed to change the data referenced through these pointers. But that doesn’t mean that this data is guaranteed not to change in other ways. The doofus123() function could change the data through the pointer mydata2, which points to the same location as mydata3. And we can’t assume that mydata and mydata2 point to different locations (if they do refer to the same data, this is called pointer aliasing), so there’s no guarantee that the data referenced by mydata won’t change.
In C++, if an object’s method is marked with const, it means that method cannot modify any of the non-mutable fields of the object, and that method can be called through a const * to the object, whereas non-const methods cannot be called via a const *:
class Dingus
{
int data;
public:
void setData(int x);
int getData() const;
};
Dingus dingus;
const Dingus *pdingus = &dingus;
int n = pdingus->getData(); // OK
pdingus->setData(33); // illegal: pdingus is a const *
You should learn to use const! It’s the key to writing software that promises not to change data. The compiler will produce an error to stop you from inadvertently violating this promise, at least if you don’t circumvent the compiler and cast away the const qualifier. In an embedded system, it also allows you to mark initializer data in such a way that it can be stored in nonvolatile program memory rather than in generally scarcer volatile data memory:
const char author[] = "James Q McGillicuddy";
Neither the const * concept in C or the const & concept in C++ (data that the compiler will not allow you to change through const pointers and references) has an equivalent in Java; the Java final keyword applies only to the direct contents of a variable itself, and it just means that the Java compiler will not allow you to assign a final field more than once.
public class Doofus
{
private int x;
public void setX(int newX) { this.x = newX; }
}
public class Dingus
{
final private Doofus doofus;
public Dingus()
{
this.doofus = new Doofus();
}
public void tweak()
{
this.doofus = new Doofus(); // illegal: doofus is final
this.doofus.setX(23); // OK, we can call any public method
}
}
Neither language provides a way to mark data as truly immutable, however; we can only hide that data behind an API that prevents cooperating software from modifying the data.
The poster child in Java of immutability, or lack thereof, is the mutable java.util.Date class. If you want to use Date objects to record the date and time of your birthday or anniversary or upcoming colonoscopy, and you allow someone else access to those objects, you are giving them a blank check to change the fields of the Date object. To be safe, you need to make a defensive copy. That’s extra work that would be unnecessary if Date had immutable fields.
In fact, there’s a whole school of thought that everything should be immutable; the functional programming languages strongly encourage the use of immutable objects. When you want to change some object X, instead of altering its data, you create a whole new object X in its place. This sounds like a lot of extra work — but anytime you think that, go look at the advantages I cited earlier with immutable data.
An Example: The Immutable Toaster
The embedded guys who deal with plain old integer data types in C are probably looking at this and scratching their heads. Objects don’t enter the picture at all, and “new object” seems to allude to dynamic memory allocation, which a lot of us in the embedded world avoid like the plague. So here’s an example; let’s write a program that controls a toaster. It has an update function that’s called 10 times a second. Oh, and we need to modulate the heating element on and off, keeping it on at most half the time, not all the time, otherwise it will be too hot and have a tendency to burn the toast.
enum ToasterState { TS_INACTIVE, TS_TOASTING, TS_READY };
typedef struct TAG_ToasterInfo {
ToasterState state;
int16_t timer;
bool heating_element_on;
} ToasterInfo;
void toaster_update(ToasterInfo *pti, bool buttonpressed, bool dooropen, int16_t dial)
{
if (pti->state == TS_INACTIVE)
{
if (buttonpressed)
{
pti->state = TS_TOASTING;
pti->timer = 0;
pti->heating_element_on = true;
}
}
if (pti->state == TS_TOASTING)
{
if (pti->timer >= dial)
{
pti->state = TS_READY;
pti->heating_element_on = false;
}
else
{
++pti->timer;
if (!pti->heating_element_on)
pti->heating_element_on = true;
if (pti->heating_element_on)
pti->heating_element_on = false;
}
}
if (pti->state == TS_READY)
{
if (dooropen)
{
pti->state = TS_INACTIVE;
}
}
}
Very simple, you turn the dial to set the toasting time, press the button, the toaster turns on and starts a timer, toggling the heating element on and off, and when the timer exceeds the dial setting then the toaster turns off and waits for you to open the door before it will start again. Not much to it!
Can you find the bugs here? They’re subtle.
One problem is that we read and write pti->state all over the place in this function, and we muddle its new and old value. By “muddle”, I mean that we update pti->state at one point in the function, and then we read its value later, when we probably meant to refer to its original value at the start of the function. In this case, the effect is not that critical; it just means the toaster finishes what it’s doing a split second earlier, depending on the order of statements within the function; if we rearrange them, we might get state transitions that occur one iteration later.
The bigger problem is in the heating element toggle code:
if (!pti->heating_element_on)
pti->heating_element_on = true;
if (pti->heating_element_on)
pti->heating_element_on = false;
This turns heating_element_on to true, but then immediately afterward, turns it to false. Again, we are muddling its new and old value.
You might think this is an obvious bug, and no sane person would write code that works that way. Why not just toggle heating_element_on:
pti->heating_element_on = !pti->heating_element_on;
Well, we could, in this case, and it would be correct. But that’s only because this is a really easy kind of behavior to design. What if we needed to do something more complicated, like run the heating element at 60% duty cycle, or if we needed to control the heating element based on a thermostat?
The problem with changing state variables in place, is that we have plenty of opportunities to write programs with errors, because the same name in a program now refers to different values, which are sensitive to the order in which we do things. Let’s say there’s some other logic in the program that needs to do something at the precise moment when the heating element is on and something else occurs. If this other logic precedes the toggle statement, then pti->heating_element_on refers to the previous heating element state, whereas if the other logic follows the toggle statement, then pti->heating_element_on refers to the next heating element state. And that’s a simple case, because there’s only one place in which the heating_element_on member is modified. In general it’s not that simple; there may be multiple places in the code where state can be modified, and if it occurs in if statements, then sometimes the state is modified and sometimes it is not. When we see pti->state or pti->heating_element_on, we can’t tell if these refer to the value of state variables as they were at the beginning of our update function, or a changed value at the end, or some intermediate transient value in the middle of calculations.
(Things get even uglier if there are complex data structures, like a linked list, where a pointer itself is modified:
plist->element.heating_element_on = true; // Line A
plist = plist->next;
plist->element.heating_element_on = false; // Line B
Here we have two lines, A and B, which both change mutable state, and the lines look the same, but they refer to two separate pieces of data.)
A better design for our toaster software uses separate data for input and output state:
void toaster_update(const ToasterInfo *pti, ToasterInfo *ptinext,
bool buttonpressed, bool dooropen, int16_t dial)
{
/* default: do what we were doing */
ptinext->state = pti->state;
ptinext->timer = pti->timer;
/* for safety: default the heating_element_on to false */
ptinext->heating_element_on = false;
if (pti->state == TS_INACTIVE)
{
if (buttonpressed)
{
ptinext->state = TS_TOASTING;
ptinext->timer = 0;
ptinext->heating_element_on = true;
}
}
if (pti->state == TS_TOASTING)
{
if (pti->timer >= dial)
{
ptinext->state = TS_READY;
ptinext->heating_element_on = false;
}
else
{
ptinext->timer = pti->timer + 1;
if (!pti->heating_element_on)
ptinext->heating_element_on = true;
if (pti->heating_element_on)
ptinext->heating_element_on = false;
}
}
if (pti->state == TS_READY)
{
if (dooropen)
{
ptinext->state = TS_INACTIVE;
}
}
}
To use this version of the update function properly, we need to avoid pointer aliasing, so that inside the function, we have complete freedom to change the contents of the next state, while still being able to assume that the contents of the existing state stays unchanged. So we can’t do this:
ToasterInfo tinfo;
tinfo.state = TS_INACTIVE;
while (true)
{
/* get inputs here */
toaster_update(&tinfo, &tinfo, buttonpressed, dooropen, dial);
/* set output here based on tinfo.heating_element_on */
wait_100_msec();
}
But we could call the update function using a pair of ToasterInfo states:
ToasterInfo tinfo[2];
ToasterInfo *ptiprev = &tinfo[0];
ToasterInfo *pti = &tinfo[1];
ptiprev->state = TS_INACTIVE;
while (true)
{
/* get inputs here */
toaster_update(ptiprev, pti, buttonpressed, dooropen, dial);
/* set output here based on pti->heating_element_on */
/* swap pointers to state variables */
ToasterInfo *ptmp = pti;
pti = ptiprev;
ptiprev = ptmp;
wait_100_msec();
}
Now when we are looking at the toaster_update() function, we can clearly distinguish the old value of the toaster state from the new value of the toaster state. And because we used const, we can have the compiler help catch our errors if we try to assign to any of the pti members instead of ptinext. Moreover, if we have the program stopped in a debugger, we can see both the previous state and the new state in their entirety, without having to do any clever sleuthing to infer this information.
This creates a little bit of extra work, but one of the key lessons of software design is that you have to make tradeoffs, and often you end up giving up a little bit of performance efficiency to gain improvements in code clarity, modularity, or maintenance.
This kind of approach (e.g. new_state = f(old_state, other_data)), where we decouple the mutable state update from the computation of new state, is something I call “pseudo-immutability”. It’s not purely immutable, since we are storing a mutable state variable somewhere, but the data looks immutable from the standpoint of computing the new state, and the software design tends to be cleaner as a result.

A Tour of Immutable Data
One key idea when considering immutability is the value type. Values are just ways of interpreting digital bits, and the important point is what they are, not where they are stored.
Let’s say you have a software program that works with a complex number e.g. 4.02 + 7.163j; this is just a way of interpreting two 64-bit IEEE-754 floating-point values, one for the real part, and one for the imaginary part. This number exists independently of where it is stored. In fact, if we want to be purely functional, there is no storage: there are only inputs and outputs.
When we do have state containing a complex number, it happens to be just a transient place to store the 128 bits. The complex numbers themselves are nomads (“Hey, I’ll bet you didn’t realize you’ve been using monads all along!” “No, I said nomads, not monads, you creep!”) traveling from place to place, stopping inside a state variable only for a microsecond. One problem with the average approaches of programming using mutable state, is that this idea of transiency disappears. Instead, we get focused on some variable z containing a complex number, that lasts for a long time, and we poke and prod at it, and the name z might refer to an erratically changing series of values.
The alternative to a value type is a reference type, where a critical aspect of the data is where it is stored. If I have persistent mutable state in a software program, like a color palette for a window manager, the data lives somewhere, and unless I want to deal with potentially out-of-date copies, when I work with that color palette, I pass around a pointer to that data. The value of the color palette is a particular fixed choice of colors. But the window manager’s reference to the color palette is a unique container for those values; it lives in one place, and its contents can change. (In C, the term lvalue refers to a storage location, which, if it does not have a const qualifier, can be used on the left side of an assignment statement; the term rvalue refers to an expression which can be used on the right side of an assignment statement.)
Microarchitecture: Low level immutable data
Perhaps when you program, you picture RAM as kind of like one of those plastic storage containers with lots of little compartments. Locations 0x3186-0x319c contain your name; locations 0x319d-0x31f2 contain your address, and so on. At a low level, this is because RAM retains state by default: as long as we keep it happy, some pattern of bits at a particular location will stay the way they are. With static RAM (SRAM), we just provide a well-conditioned source of power; with dynamic RAM (DRAM), we have to activate refresh circuitry, which used to be part of the overall system design in a computer, but is now an intrinsic part of the memory module itself. In either case, the RAM requires an explicit write step to change its contents. On the other hand, if you look at the registers and data paths inside a processor, they are very functional in nature. Here’s the block diagram of the Microchip PIC16F84A microcontroller, from the datasheet:
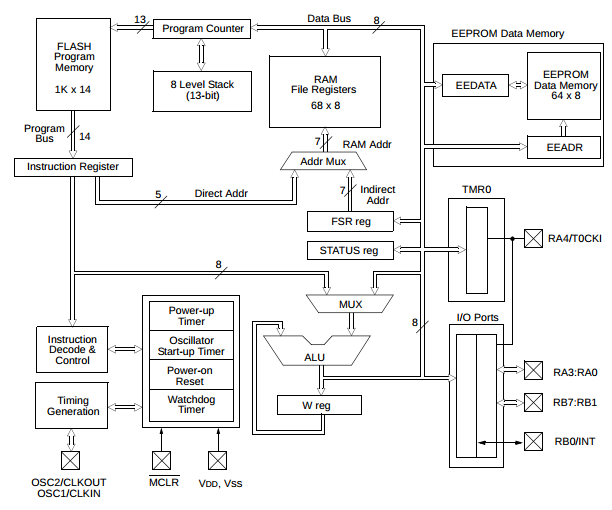
The 16F84A has a register file for its data memory. The difference between a register file and SRAM is kind of a gray area that depends on the architecture and implementation. The classical definition of a register file is a small group of registers (one for each address in the register file) with separate input and output data ports; we can think of a register as a tandem group of D flip-flops, which are clocked data storage devices: during a particular clock cycle, the output of a flip-flop is constant, but at the rising edge of the clock signal, the D flip-flop’s input is captured by the flip-flop and propagated to the output during the next cycle. Memory in a D flip-flop is transient and only lasts for 1 clock cycle. If you want the data to persist in value, you have to feed the output back to the input. (Those of you who are more familiar with DSP than digital design can think of a register or a D flip-flop as a unit delay z-1.)
So a register file can be thought of as a bunch of D flip-flops and multiplexers: If you are writing new information to the register file to a particular location, the multiplexer for that register gets its data from the register file’s input port, whereas if you’re not writing to the register file, the multiplexer maintains each register’s value by getting its data from the previous value of the register.
The special-purpose registers of the 16F84A, like the program counter or the W register, are similar, but they have manually-designed data paths:
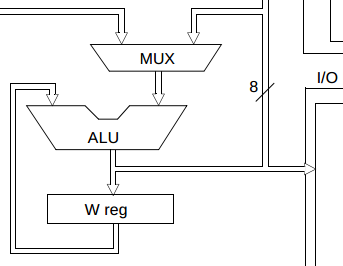
The W register is an 8-bit register which is always a function of its previous value and some other data. The exact function used depends on the arithmetic-logic unit (ALU). And this pattern is essentially the same as the “pseudo-immutable” approach I have been talking about:
new_state = f(old_state, some_other_data);
This keeps new and old state conceptually separate, as opposed to the average old mutable approach that causes us headaches:
// "state" refers to old values
if (some_condition)
{
state.some_member = state.some_member + something_else;
}
// now "state" refers to new values
if (other_condition)
{
state.other_member = state.some_member - another_thing;
}
// now "state" has changed again
So it’s not just the Functional Wizards who are using immutable data; at a low level, many microprocessors and microcontrollers utilize the same approach of separating input and output data.
Immutable Data Structures
Back to the high level of programming: there’s a whole subject of immutable or persistent data structures. The idea is that you don’t change the contents of data; instead, you create a new set of data.
This may seem wasteful and impractical, and in some cases it is. For example, if you have an array X of 1 million integers, and you want to change the 30257th element of X, it takes a lot of work just to create a new array with a new value for element #30257 and copies of all the other elements of X. Then if you don’t need the old array any more, you throw it away. Wasteful… except that general-purpose computers are fast and have lots of memory, and the high-level languages recycle unused memory through garbage collection. In Python, the numpy library uses optimized C code underneath to manipulate arrays, and although mutable data access is supported, there are many numpy methods that are functional in nature and create new copies of data rather than changing state in-place. The advantages usually outweigh the costs; we can design programs with fewer errors, and by separating input and output we can optimize the computation, by using parallel computations or a GPU to speed up functional programming, whereas mutating state prevents many of these optimizations.
But arrays are only one type of data structure.
For most of the usual mutable data structures, there are immutable equivalents. The classic example is the list. A mutable list might rely on a linked list implementation. Immutable lists also use linked lists, but they have that nice property, like any other immutable data structure, that the nodes of an immutable list won’t change. Here’s an example in Java:
public class ConsList<T>
{
private final T car;
private final ConsList<T> cdr;
public ConsList(T car, ConsList<T> cdr)
{
this.car = car;
this.cdr = cdr;
}
public T head() { return this.car; }
public ConsList<T> tail() { return this.cdr; }
}
Really simple: a list consists of one item (the head() of the list) and a reference to the rest of the list (the tail()). The names cons and car and cdr are weird names that date back to old LISP implementations, and perhaps it would have been better to get rid of cons, and use first and rest:
public class ImmutableList<T>
{
private final T first;
private final ImmutableList<T> rest;
public ImmutableList(T first, ImmutableList<T> rest)
{
this.first = first;
this.rest = rest;
}
public T head() { return this.first; }
public ImmutableList<T> tail() { return this.rest; }
}
If we wanted to store the list (1,2,3,4) we would do it this way:
ImmutableList<Integer> list1 =
new ImmutableList<Integer>(1,
new ImmutableList<Integer>(2,
new ImmutableList<Integer>(3,
new ImmutableList<Integer>(4,
null))));
We can visualize the list nodes as follows. Each contains a pair of references, one to the list head and the second to the remaining elements, with the end of the list denoted by a link to null:
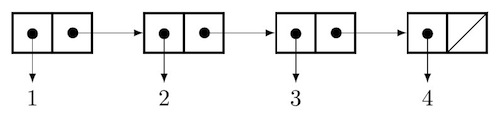
Insertion at the beginning is easy:
ImmutableList<Integer> list2 =
new ImmutableList<Integer>(5, list1);
// this is the list (5,1,2,3,4)
Decapitation (removal of the head) is also easy:
ImmutableList<Integer> list3 =
list1.tail();
// this is the list (2,3,4)
While these three lists are conceptually separate, they reuse many list nodes.
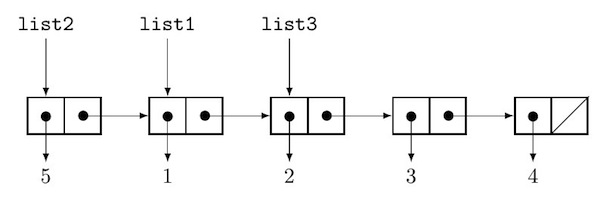
In fact, the reason these are called persistent data structures, is because the immutability of the data means that you can keep around references to older versions, and they will be unaffected by the changes to the data structure, since really there are no changes, only new structures made of nodes which may be newly allocated or may be shared with other immutable data.
Other operations (appending, or insertion/removal of interior nodes) are possible but require extra list node copies and take longer to finish. In Java, this type of list is a bit verbose to manipulate; in functional languages like LISP or Haskell, list node concatenation is a primitive operation that is much shorter to write in code.
Other data structures like queues, maps, trees, are also possible to implement using immutable techniques. There has been a great deal of research on efficient implementations of these structures, including so-called “amortized algorithms” for reducing the worst-case execution time for things like binary tree rebalancing, by spreading the occasional long operation into many short operations that extend into the future. It’s just like a home mortgage: instead of having to come up with $399,000 in one fell swoop, we go to the bank and get a 30-year 4.5% mortgage with a monthly payment of $2001. We can keep our worst-case costs per operation low by spreading them out over time.
The catch with this whole technique — whether you use complex amortized algorithms, or a simple list with cons cells — is that you need to use dynamic memory allocation, and you need to have some way of recycling unused data, namely reference counting or garbage collection. And that means that while it works great for high-level languages, in low-level languages like C or even C++, immutable data structures are difficult to manage. In C++ there are possibilities (C++11 introduced shared_ptr<> to facilitate automatic memory management; before C++11 the Boost libraries can be used for their own shared pointers); you can read about some of them in these articles.
So immutable data structures are probably out of the running in the low-level embedded world, at least until someone invents a technique for automatic memory management, that also satisfies the hard real-time, determinism, and/or memory safety requirements of many applications.
Loops?
We’ve talked about the pseudo-immutable approach of isolating updates of mutable state from the computation of new state:
new_state = f(old_state, some_other_data);
There are other ways of enhancing immutability in software design. One of them involves control flow. Take, for example, the simple for-loop in C:
for (int i = 0; i < L; ++i)
{
do_something(i);
}
Here we have a mutable loop variable i. C++ uses a similar approach with STL iterators to facilitate iteration over a generic container, by overloading the increment operator ++ and the pointer dereferencing operator *:
std::vector<Something> mydata = ...;
for (std::vector<Something>::iterator it = mydata.begin();
it != mydata.end();
++it)
{
do_something(*it);
}
Again, a mutable loop variable. And there’s nothing really wrong with it, but if you get a warm happy feeling from functional-style programming, you will not get a warm happy feeling from these programming snippets. The STL use of immutable iterators are a little clumsy (::const_iterator vs ::iterator), and there’s always a risk with more complex software that you might accidentally put another ++it somewhere by mistake, and unintentionally increment the loop twice when you really meant just to do it once. The compiler won’t catch your mistake, as it allows you to modify the loop variable in the body of the loop, and it has no way of figuring out what you really wanted.
There are two approaches for removing mutable loop variables. One is recursion. LISP and other functional languages encourage the use of recursion rather than looping. Here’s an example in Java that uses the ImmutableList<T> type I described earlier:
/* Find the sum of a list's elements.
* (Let's forget about overflow.)
*/
int sum(ImmutableList<Integer> list)
{
if (list == null)
{
return 0;
}
else
{
return list.head() + sum(list.tail());
}
}
Simple! To find the sum of the elements of a list, it’s either 0 for an empty list, or it’s the head of the list plus the sum of the remaining elements. No loop.
So what’s the catch? It’s this line:
return list.head() + sum(list.tail());
We have to use recursion, which means that if a list has N elements, we need to use up N stack frames. This imposes a memory cost for the stack, and means that if we are debugging and put a breakpoint somewhere for a 1000-element list, there might be 1000 stack frames for us to scroll through in the debugger. Yuck. But that’s not fair, because we know we can solve the same problem with an iterative approach that only uses 1 stack frame:
int sum(ImmutableList<Integer> list)
{
int result = 0;
ImmutableList<Integer> p = list;
while (p != null)
{
result += p.head();
p = p.tail();
}
return result;
}
The functional languages have a feature called tail recursion in which the compiler or interpreter is smart enough to recognize recursion that doesn’t require additional stack frames; instead of pushing the return address on the stack and then calling the function again, it sets things up to jump back to the beginning of the function, effectively forming an iterative implementation of a recursive solution. Sometimes the compiler or interpreter is smart enough to do everything on their own; other times it has to be helped by writing code that is amenable to tail recursion. Our example isn’t:
return list.head() + sum(list.tail());
The problem is that we have to first make a recursive call to sum(), then add the head of the list. Adding the head of the list is a deferred action that blocks us from performing tail recursion, because there’s still something to do after the recursion completes. Here’s a modification:
/* Find the sum of a list's elements.
* (Let's forget about overflow.)
*/
int sum(ImmutableList<Integer> list)
{
return sum_helper(list, 0);
}
int sum_helper(ImmutableList<Integer> list, int partial_sum)
{
if (list == null)
{
return partial_sum;
}
else
{
return sum_helper(list.tail(), partial_sum+list.head());
}
}
In this case, we can handle the addition step before we recurse. The recursion is the last thing, therefore we can theoretically just jump back to the beginning of sum_helper() and not have to waste unnecessary stack frames. But it requires the language implementation to perform tail call optimization, and neither C nor Java appear to guarantee that they will do so, although presumably some C compilers will and maybe Java will in a future version.
The approach I like better is the one used in Python, where instead of recursion, we have a for-loop construct where the iteration is managed within the language:
for item in collection:
do_something_with(item)
Here we have to implement collection in a special way so that the language understands how to iterate over its items. (In Python it’s the iterator protocol.) The language will take care of executing the loop body, with the item variable bound to each item of the collection in sequence. If Python supported immutable data, we could make the loop variable item immutable: even though it takes on different items each time around the loop, within each loop iteration it is intended to be constant.
Of course, in our sum example we would still need to use a mutable state variable:
mysum = 0
for item in collection:
mysum += item
The purely functional alternatives are to use tail recursion, or higher order functions like reduce() or fold() to combine the elements of a collection. We just have to come up with a user-defined function that specifies how each element is supposed to be combined with the result.
Does it matter? Well, yes and no. The mutable approach in this case (mysum += item) is really simple, and it’s very clear to the reader what is going on, so there’s no strong reason to use functional techniques. But in more complicated cases, the functional approaches can lead to a more organized approach that helps ensure correctness. Let’s say we wanted to sum the square of all values which are divisible by 3:
mysum = 0
for item in collection:
if item % 3 == 0:
mysum += item*item
That’s not so bad either… but it’s starting to get more complicated. Functional approaches create a pipeline:
mysum = sum(square_map(div3_filter(collection)))
where we’d have to define functions square_map that yields a new list with squared values, and div3_filter yields a new list of only the items which are divisible by 3. We can either write them manually, or use the higher-order functions map() and filter(). In Python we can do this more concisely with list comprehensions or generator expressions:
sum(item*item for item in collection if item % 3 == 0)
If you’re used to comprehensions, this is very clear and concise. If you’re not, it seems weird, and the original combination of for and if statements would be better. They’re essentially equivalent. You say po-TAY-to, I say po-TAH-to. The difference is that in the functional approach, I don’t have to keep track of the intermediate state involved in the accumulation of sums. And if that doesn’t matter, then pick whichever approach you and your colleagues like best. But sometimes, handling all the housekeeping of intermediate state can be rather cumbersome.
Perhaps the simplest example of how intermediate state makes programming more complex is the swap operation. In Python we can use destructuring assignment:
a,b = b,a
Simple and clear! If we could only assign to one value at a time, we’d be stuck with using a temporary variable:
tmp = a
a = b
b = tmp
That’s fairly simple as well, but then I have to stop and think if I did that right, and Doubt enters my mind, and I think that maybe I should have used this logic instead:
tmp = a
b = tmp
a = b
Hmm. (In case you’re wondering, this second attempt is wrong; the previous code snippet is the correct one.)
In any case, there’s a theme here. To help yourself avoid errors, keep things clear and simple, and removing unnecessary mutable state is often a way to keep things clear and simple.
Shared Memory?
Another reason for considering immutability involves shared memory. With multiple threads or processes, shared memory is a common technique for using state with concurrent processing. But it imposes a cost, namely of using locks or mutexes to ensure exclusive access.
The immutable way of handling shared state is… well, it’s to avoid sharing state at all. No shared state means no locks. And the classic way to get there is to use message passing. Erlang is probably the prime example of a language with built-in message-passing support, and nearly all GUI frameworks use message queues.
For example, if I had three threads in a software application that needed access to a database, rather than using a lock on the database so only one thread could access it at a time, I could allow none of the threads to have direct access to the database, and instead require these threads to interact with a database manager by sending messages to it. The result is that I never have to share mutable data between threads.
The cost of message-passing is maintaining a message queue, but there are some fairly simple algorithms (such as the non-blocking one described by Michael and Scott) which guarantee proper concurrent access to a queue. Also, if we’re going to use message-passing to overcome the need for shared data, we must use value types: we have to send the data directly. We can’t send pointers to data, since that would require the data to be directly addressable by more than one thread or process, and that would require shared data. Any type of reference that can be sent via message passing (like an array index or a lookup key) must be meaningful to both the sending and receiving entity.
Here’s another example: let’s say we had 10 worker threads, and wanted to use each of them to analyze some fragment of data, and boil the analysis down to a number and add it in to a cumulative total. The shared memory approach looks something like this for each worker thread:
partial_sum = compute_partial_sum(data)
try:
lock(shared_sum_lock)
shared_sum += partial_sum
finally:
unlock(shared_sum_lock)
The message passing approach looks like this:
# Worker thread:
partial_sum = compute_partial_sum(data)
send_message(main_thread, 'partial_sum', my_thread_id, partial_sum)
# Main thread
sum = 0
nthreads = 10
while nthreads > 0:
(message_tag, thread_id, contents) = message_queue.get(block=True)
if message_tag == 'partial_sum':
nthreads -= 1
sum += contents
With the shared memory approach, we rely on each of the worker threads to operate correctly. If any of them hangs or crashes before unlocking the shared resource, the whole system can deadlock. With the message-passing approach, we don’t have to worry about this. The only way the whole sum can screw up is if the main thread hangs or crashes; otherwise, the worst outcome is that we might not hear from one of the worker threads, and we can deal with this by rewriting the main thread to time out, and either give up or restart a new worker thread on the missing data.
Pure functional approaches for managing state
There’s no perfect answer for when to use mutable data and when to use immutable data. The extreme case of eliminating all mutable data whenever possible, is something that is used in some functional programming environments. In Haskell, for example, you have to go out of your way to use mutable objects. And that means you’re probably going to have to talk to the guy in the corner about monads. Or talk to one of the other guys, who are less intimidating, about them. There are a lot of good reasons why they are useful, it just takes quite a bit of mental energy to figure out what’s really going on.
return :: a -> Maybe a
return x = Just x
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
m >>= g = case m of
Nothing -> Nothing
Just x -> g x
When you understand them well enough that they’re intuitive for you to use, let me know what you learned.
Wrap-up
Here’s a summary of what we talked about today:
- Using immutable data simplifies software design, removing problems for shared access and concurrency, and removing the need for defensive copies.
- Some programming languages include support for some aspects of immutability, like
constin C/C++ andfinalin Java, but these generally don’t provide full immutability. - Pseudo-immutable techniques are a good real-world compromise to reduce the chances of human error, by decoupling the state update from the computation of its new value, rather than changing mutable state in place:
new_state = f(old_state, other_data) - The registers in low-level microarchitectures use the pseudo-immutable approach, with flip-flops forming the propagation from old state to new state.
- Immutable (aka “persistent”) data structures can support the use of immutability to create versions of lists, maps, queues that have the advantages of immutability.
- Functional techniques of recursion and iteration are alternatives to looping with mutable state variables.
- Message-passing leverages immutability to eliminate the concurrency problems of shared memory.
- You can use monads if you want to turn to pure functional techniques. (“Hey, I’ll bet you didn’t realize you’ve been using monads all along!”) Remember, I said you can use monads. I probably won’t, at least not intentionally.
Whew! That was longer than I had intended. The next article is on volatility and is much shorter.
© 2014 Jason M. Sachs, all rights reserved.
- Comments
- Write a Comment Select to add a comment
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:























